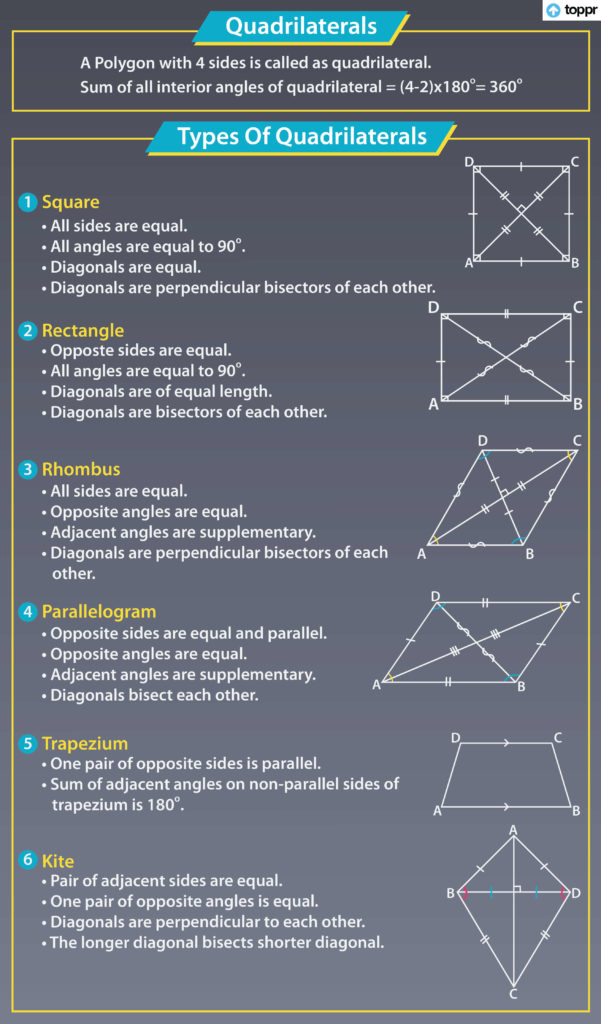
We all know that quadrilaterals are four-sided closed figures. Every quadrilateral is given a special name depending on the properties specific to their shape. Trapezium and Kite are also types of quadrilaterals with properties specific to their shapes. In the chapter below we will discuss the varying properties of a trapezium and kite.
Suggested Videos
Trapezium and Its Properties
A trapezium or a trapezoid is a quadrilateral with a pair of parallel sides. A parallelogram may also be called a trapezoid as it has two parallel sides. The pair of parallel sides is called the base while the non-parallel sides are called the legs of the trapezoid. The line segment that connects the midpoints of the legs of a trapezoid is called the mid-segment.

Every trapezium shows the following properties:
- Angle: The sum of angles in a trapezoid-like other quadrilateral is 360°. So in a trapezoid ABCD, ∠A+∠B+∠C+∠D = 360°.
- Two angles on the same side are supplementary, that is the sum of the angles of two adjacent sides is equal to 180°.
- The length of the mid-segment is equal to 1/2 the sum of the bases. In the above figure mid-segment= 1/2 (AB+CD)
- In special cases of the isosceles trapezium, legs of the trapezium are congruent to each other. This means that despite being non-parallel, the measurement of both the legs is equal.
Browse more Topics under Understanding Quadrilaterals
- Polygon and Its Types
- Angle Sum Property of Polygons
- Properties of Parallelogram, Rhombus, Rectangle and Square
You can download Quadrilaterals Cheat Sheet by clicking on the download button below
Kite and Its Properties
Kite is also a quadrilateral as it has four sides. Being a special type of quadrilateral, it shows special characteristics and properties which are different from the other types of quadrilaterals. A kite is the combination of two isosceles triangles. Let’s see how!

In a kite, two adjoining sides are equal as shown in the figure. These sides are called as distinct consecutive pairs of equal length. From the above discussion we come to know about the following properties of a kite:
- Two pairs of sides known as consecutive sides are equal in length.
- One pair of diagonally opposite angles is equal in measurement. These angles are said to be congruent with each other.
- The diagonals meet each other at 90°, this means that they form a perpendicular bisection.
From the above discussion, we can now differentiate the peculiar shapes of trapezium and kite.
Solved Question for You
Question: Find the value of y in the given figure

Solution: Mid-segment of the trapezium = 1/2 (Base1 +Base2)
Base1 of the trapezium = 12
Base2 of the trapezium= 18
So, Mid-segment = 1/2 (12+18) =1/2(30) =15
Now, we know the measurement of the mid-segment which equals 2y-1
2y-1=15
2y=15+1=16
y=8
So the value of y= 8.
Question. Explain what makes a trapezium a trapezium?
Answer. A trapezium is characterized by the properties it does not possess. Furthermore, it has no parallel sides. In case the quadrilateral had one pair of parallel sides, it will be characterized as a trapezoid. In case both pairs of sides happen to be parallel, the figure would be a parallelogram.
Question. What is the formula for calculating the trapezium area?
Answer. The formula for computing the area of a trapezium is 1/2× Sum of parallel sides × distance that exists between them.
Question. Can we say that the diagonals of a trapezium are equal?
Answer. Diagonals are equal only in the special case of trapezium that is known as a trapezoid (or isosceles trapezium). Furthermore, a characteristic property of trapezoid is that the diagonals happen to be equal. It is certainly not a necessity that diagonals of all types of trapezium turn out to be equal.
Question. Which angles happen to be equal in a trapezium?
Answer. The sum of angles in a trapezoid-like other quadrilateral happens to be 360°. Therefore, in a trapezoid ABCD, ∠A+∠B+∠C+∠D will be 360°. Two angles on the same side happen to be supplementary.







jhi;gío/o =]41#