Gravitational Force Formula

After Newton discovered the gravity people came to know about gravity. Furthermore, now a day’s everybody knows what is gravity. But, do you also know that right now you are pulling on every other object in the universe? So, to find out more go through the topic to learn about gravitational force, gravitational force formula, formula’s derivation and solved example.

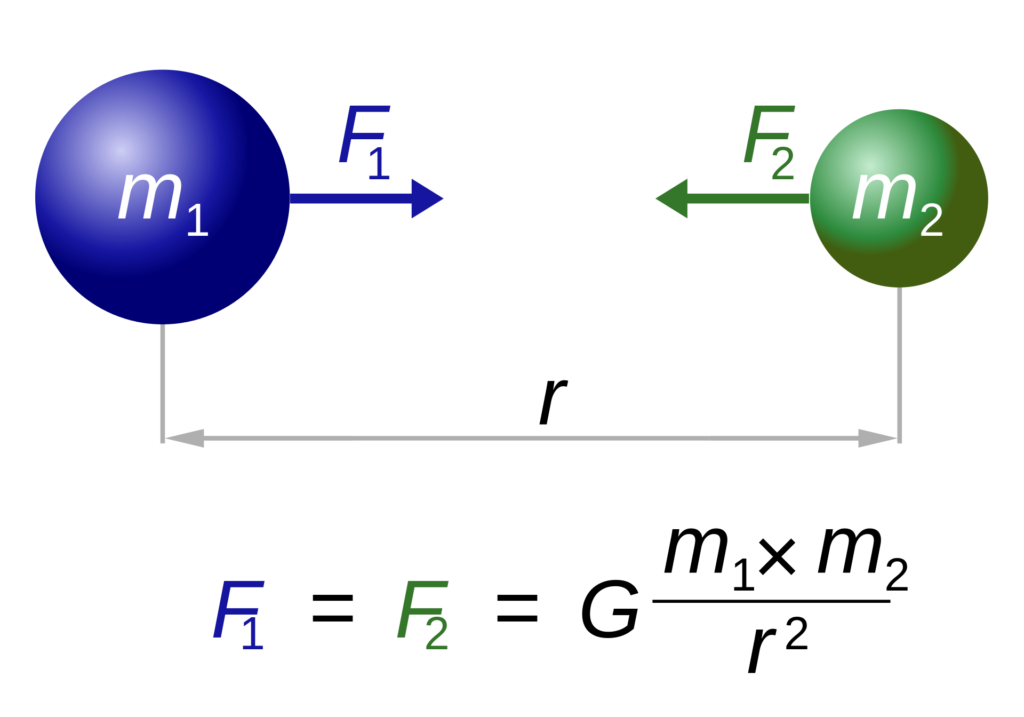
Gravitational Force

In the universe, there are many forces, a lot of pushes and pulls. Moreover, we are always pulling or pushing something, even if only in the ground. But, actually, in physics, there are four fundamental forces from which everything else is derived. Besides, these forces are the weak force, the strong force, the gravitational force, and the electromagnetic force.

Furthermore, the gravitational force is something that attracts any two objects with the mass. In addition, this gravitational force attracts because it always tries to pull masses together and it never pushes them apart. Moreover, every object including you pulls every other object in the entire universe and this is called Newton’s Universal Law of Gravitation.

Get the huge list of Physics Formulas here

Gravitational Force Formula

The gravitational force formula is also known as Newton’s law of gravitation. Also, it defines the magnitude of the force between two objects. Furthermore, the gravitation force formula includes the gravitational constant whose value is G = 6.67 \(\times 10^{-11} N \cdot m^{2}/ kg^ {2}\). Besides, the unit of gravitational force is Newtons (N).

gravitational force = \(\frac{(gravitational constant) (mass of object 1) (mass of object 2)}{(distance between objects)^{2}}\)

\(F_{g}\) = \(\frac{Gm_{1}m_{2}}{r^{2}}\)

Derivation of the Gravitational Force Formula

\(F_{g}\) = refers to the gravitational force between two objects (N = \(kg \cdot m/s^{2}\))
G = refers to the gravitational constant (G = 6.67 \(\times 10^{-11} N \cdot m^{2}/ kg^ {2}\))
\(m_{1}\) = refers to the mass of the first object in kilogram
\(m_{2}\) = refers to the mass of the second object also in kilogram
r = refers to the distance between the object in meters

Solved Example

Example 1

Suppose two satellites that orbit the earth passes close to each other. Also, for a moment they are 100 m apart. Furthermore, the masses of the satellites are 300 kg and 20 kg. So, calculate the magnitude of the force of gravity between these satellites?

Solution:

We can calculate the magnitude of the force between two satellites using the gravitational force formula:

\(F_{g}\) = \(\frac{Gm_{1}m_{2}}{r^{2}}\)

\(F_{g}\) = \(\frac{(6.67 \times 10^{-11} N \cdot m^{2}/ kg^ {2}) (300 kg) (20 kg)}{(100 m)^{2}}\)

\(F_{g}\) = \(\frac{(6.67 \times 10^{-11} N \cdot m^{2}/ kg^ {2}) (6000 kg^{2})}{10000 m^{2}}\)

\(F_{g}\) = \(\left ( 6.67\times 10^{-11}N\cdot \frac{m^{2}}{kg^{2}} \right ) \times \frac{6000 kg^{2}}{10000 m^{2}}\)

\(F_{g}\) = \(\left ( 6.67\times 10^{-11}N\cdot \frac{m^{2}}{kg^{2}} \right ) \times \left ( 0.6000\frac{kg^{2}}{m^{2}} \right )\)

\(F_{g}\) = \(\left ( 6.67\times 10^{-11}N\cdot \frac{m^{2}}{kg^{2}} \right ) \times \left ( 0.6000\frac{kg^{2}}{m^{2}} \right )\)

\(F_{g}\) = (\(6.67\times 10^{-11}N) \times\) (0.600)
\(F_{g}\) \(\cong \) \(4.00 \times 10^{-11}N\)

So, the magnitude of the gravitational force between the two satellites when they were at a distance of 100 is \(4.00 \times 10^{-11}N\) (Newtons).

Example 2

Scientist put an experiment to measure the gravitational force using two large spheres. In addition, both the spheres are 1000.0 kg, and their centers of mass are 2000.0 m apart. Now, calculate the gravitational force between these two spheres?

Solution:

So, by using gravitational formula we can find the force of gravity amid the spheres:

\(F_{g}\) = \(\frac{Gm_{1}m_{2}}{r^{2}}\)

\(F_{g}\) = \(\frac{(6.67 \times 10^{-11} N \cdot m^{2}/ kg^ {2}) (1000 kg) (1000 kg)}{(2000 m)^{2}}\)

\(F_{g}\) = \(\frac{(6.67 \times 10^{-11} N \cdot m^{2}/ kg^ {2}) (1.0000 \times 10^{6} kg^{2})}{4000 m^{2}}\)

\(F_{g}\) = \(\left ( 6.67\times 10^{-11}N\cdot \frac{m^{2}}{kg^{2}} \right ) \times \frac{1.0000 \times 10^{6} kg^{2}}{4.000 m^{2}}\)

\(F_{g}\) = \(\left ( 6.67\times 10^{-11}N\cdot \frac{m^{2}}{kg^{2}} \right ) \times \left ( 2.5000 \times 10^{5} \frac{kg^{2}}{m^{2}} \right )\)

\(F_{g}\) =\( \left ( 6.67\times 10^{-11}N\cdot \frac{m^{2}}{kg^{2}} \right ) \times \left ( 2.5000 \times 10^{5} \frac{kg^{2}}{m^{2}} \right )\)

\(F_{g}\) = \((6.67\times 10^{-11}N) \times (2.5000 \times 10^{5}\))

\(F_{g}\) = \(16.675 \times 10^{-6} N\)
\(F_{g}\) = \(16.675 \times 10^{-5} N\)

So, the magnitude of the gravitational force amid two spheres is \(16.675 \times 10^{-6} N\).