Hello Friends! Today we will look into and discuss the Ideal gas equation. We will also learn and understand the definition of Absolute Temperature and its utility in the study of Thermal properties of matter. Let us also learn what Boyle’s law is. So let us begin with the basics.
Suggested Videos
Ideal Gas Equation
To understand the ideal gas equation we will have to be clear the concepts given below.
What is an Ideal Gas?
An ideal gas is a theoretical gas! It does not exist in reality but is assumed to exist for the purpose of simplifying calculations. It also generates a reference point in relation to which the behavior of other gases can be studied.
An ideal gas is defined as a gas composed of randomly moving particles as all gases do, the only difference being that for an ideal gas when its particles collide with each other, these collisions are assumed to be perfectly elastic which means no energy of either of these particles is wasted.
In reality, however, when actual gas particles collide with each other, some of their energy is wasted in changing directions and overcoming friction. However, at STP (defined below) conditions most natural gases act just like an ideal gas subjected to reasonable restrictions.
Generally, any gas behaves similarly to an ideal gas under the conditions of high temperature and low pressure. To derive correctly the ideal gas law, we will learn some of the other very important laws for gases.
Browse more Topics under Thermal Properties Of Matter
- Calorimetry
- Change of State
- Heat Transfer
- Newton’s Law of Cooling
- Specific Heat Capacity
- Temperature and Heat
- Thermal Expansion
You can download Thermal Properties of Matter Sheet by clicking on the download button below

Boyle’s Law
Boyle’s Law states that ‘The absolute pressure exerted by a given mass of an ideal gas is inversely proportional to the volume it occupies if both the temperature and amount of gas remain unchanged’. In mathematical terms this law is given as:
P \( \propto \) 1/V or that PV = K
where P=Pressure of the gas; V=Volume of the gas; K=constant. It means that both the pressure and volume of a given mass of gas are inversely proportional to each other at a constant temperature. Furthermore, it also expresses that the product of pressure and volume for any gas is a constant and thus can be used to study the comparison of the gas under different conditions as:
P’V’ = P”V”
where both the products are for the same gas but under different pressures and volumes.
Charles’ Law

Charles’ law states that ‘ When the pressure of a sample of air is held constant, then the volume of the gas is directly proportional to its temperature‘, that is
V \( \propto \) T
where V= Volume of a gas sample; T= Absolute temperature. Quite simply put, it says that Gases expand on heating and contract on cooling.
Avogadro’s Law
Avogadro’s law states that ‘Equal volumes of all gases at conditions of same temperature and pressure have the same number of molecules’, written as:
V \( \propto \) n or V/n =K
where V=volume of gas; n=Number of moles (1 mole=6.022 x 1023 molecules). It implies that under similar conditions of pressure, volume and temperatures all gases will have an equal number of molecules, independent of the weight and density of the gas.
Ideal Gas Equation
If we combine the results of all the above gas laws we get an equation that holds true for an ideal gas. The most common form of this equation is since PV= K and V/T =k then
PV/T = constant
Thus, the Ideal Gas Equation is given as
PV = nRT
where P= pressure of the gas; V=volume of the gas; n= Number of Moles; T=Absolute temperature; R=Ideal Gas constant also known as Boltzmann Constant = 0.082057 L atm K-1 mol-1.
Using this equation, the study of any gas is possible under assumptions of STP conditions and subjecting the gas to reasonable restrictions to make it behave similarly to an Ideal gas.
What is an STP condition?
STP is short for ‘Standard Temperature and Pressure’. STP condition is defined (as per the International Standard Metric Conditions) as the surrounding absolute temperature of 288.15 Kelvin (15° Celcius) and a pressure of 1 atmosphere i.e. 1 bar or 101.325 Kpa.
What is Absolute Temperature?
Thermodynamic temperature, which is also known as ‘Absolute Temperature’ is a basic parameter for the study of thermal properties of matter.
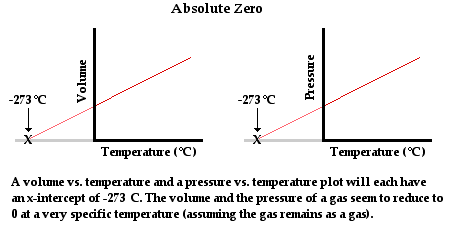
[Source:physicsclassroom]
Using an ideal gas equation we can use gas for measuring temperature accurately. Again, as this law is universal in nature, all gases can be used to get the accurate temperature irrespective of their masses and other physical properties.
However, in actual use, it is observed that real gases often deviate from this law as compared to an ideal gas. But over a wide temperature base, all real gases more or less follow a linear path as can be seen in the case of gases taken above with pressure on the Y-axis and temperature on the X-axis.
Assuming that gases continue to be in a gaseous state at lower temperatures we can extrapolate the lowest minimum temperature for a gas. This lowest possible temperature is called Absolute Zero. The temperature is obtained at -273.15° Celcius on the Celcius scale.
It is also responsible for the creation of a new temperature scale called as ‘Kelvin’ scale where absolute zero is taken as 0 and so this scale is also called as Absolute temperature scale. It is represented as Kelvin. Thus,
T(Celcius) = T(Kelvin) + 273.15
This conversion helps to determine the absolute temperature of a gas under study. Thus, we have finally derived the Ideal Gas equation after studying all the concepts involved which make up the gas laws. Thorough knowledge of these concepts is paramount to ensure the proper understanding of properties of a gas being subjected to thermal study and thus its applications.
Solved Examples for You
Question: How many moles of ‘He’ are contained in a 6-litre canister at 101 KPa and 27 ° C. Take R= 8.314 J/mol K
Solution: Using the Ideal gas equation, n = PV/RT
Therefore, on substituting the values(T = 27 + 273 = 300) we get,
= 101 x 6/ 8.314 x 300 = 606/2494.2 = 0.2429 moles
Hence, 0.2429 moles of ‘He’ are contained in a 6-litre canister at 101 KPa and 27 ° C






Leave a Reply