Variation

Variation can be clear and understandable when one first understands what are variables. Therefore, it is also important to know how they differ from constants. When the value of a quantity does not change under different conditions, it is constant. On the contrary, when the value of a quantity changes under varying conditions, it is a variable.

Introducing Variation

Mathematical equations display some type of parameters when it established a relationship. There are normally two types of quantities exist. One is constant. It doesn’t change with the changes in other parameters in the equation.

However, others are the variables which change in different situations. The changing of variable parameters is often gone by the term variations or algebraic variations.

Let’s explain with an example of a simple equation y = mx wherein m refers to a constant. Further, if we assume that the value of m is 5, then, in this case, the equation becomes y = 5x.

Similarly, when x = 1, y = 1 × 5 = 5

Further, when x = 2, y = 2 × 5 = 10

And when x = 3, y = 3 × 5 = 15

By simply changing the value of y, x gets different values as well. This is the variation of y with different values of x and similarly you can show that with different values of y the value of x changes.

Variations can be of different types according to the pattern of changing or relationships of variables.

Types of Variation

In a variation if variables change proportionately i.e. they either increase or decrease together then it is direct variations. Therefore, if X is in direct variation with Y, then you can symbolically write it as X α Y.

In inverse or indirect variations, the variables change disproportionately. Further, this means that when one of the variables increases, the other one decreases. So the behavior of the variables is just the opposite of direct variations. Therefore, if X is in indirect variations with Y, then you can symbolically write it as X α 1Y.

If more than two variables share a direct relationship or one variable changes with the change product of two or more variables, it is joint variations. Therefore, if X is in joint variation with Y and Z, you can symbolically write it as X α YZ.

Combined variations are a combination of direct, joint and indirect variations. So, in this case, three or more variables exist. Therefore, if X is in combined variation with Y and Z, you can symbolically write it as X α YZ or X α ZY.

When two variables are in relation with a formula or a variable is related by the sum of two or more variables, then it is a partial variation. X = KY + C (where K and C are constants) is a straight line equation which is an example of partial variation.

Solved Questions on Variation

If y varies directly as x, and x = 12 when y = 9, what is the equation that describes this direct variation?

k =  = 
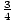
y = 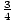x

If y varies directly as x, and the constant of variation is k = 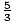, what is y when x = 9?

y = 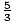x = 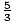(9) = 15

Further, k is a constant for every point. This means that the ratio between the y-coordinate of a point and the x-coordinate of a point are constant. Thus, given any two points (x₁, y₁)and (x₂, y₂) that satisfy the equation, 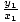 = k and  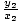= k. Consequently,  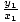=  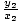for any two points that satisfy the equation.