Midpoint Formula

In coordinate geometry, we know about the Cartesian plane and representation of point using the coordinate system. Thus many times we need to find the location of the midpoint between two points. Also, the Midpoint of a line segment may be required. This midpoint will work as the center point of a straight line. Sometimes we will need to find the number that is half of two particular numbers. In that similar manner, we use the midpoint formula in coordinate geometry to find the halfway number of two coordinates. In this article, the student will learn about the concept of midpoint and midpoint formula with examples. Let us begin learning!

Midpoint Formula

Definition of Midpoint:

Midpoint formula is a mathematical equation that is used to locate the halfway point between two data points. Besides in geometry, the study of economics uses this calculation to find the coefficient of elasticity, etc. Therefore, we can say that it is used to calculate how consumer habits change as price, quantity demanded, and quantity supplied changes.

This equation is used to solve the elasticity of demand and supply in various scenarios of different models. The key characteristic of this equation is that it calculates the percentage changes based on the difference between the beginning and the ending values.

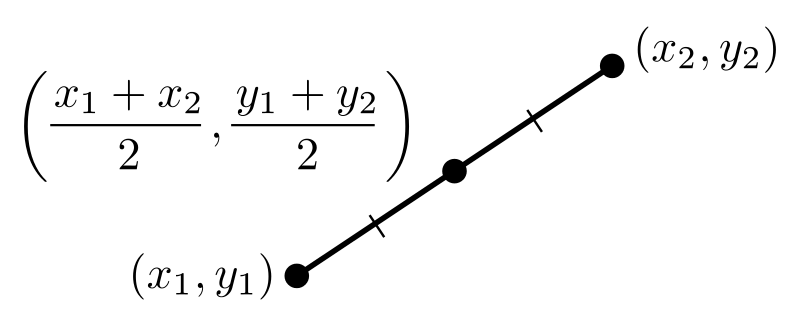
Formula to Find the Midpoint:

To find the midpoint of the straight line in a graph, we use this midpoint formula that will enable us to find the coordinates of the endpoint of the given line. Suppose the endpoints of the line is \((x_1, y_1)\) and \((x_2, y_2)\)  then the midpoint is given as:

The Midpoint Formula is given as,

\((x,y) = [\frac{x_1+x_2}{2},\frac{y_1+y_2}{2}]\)

Where, \(x_1, x_2\) are the coordinates of the x-axis. \(y_1, y_2\)  are the coordinates of the y-axis.

Similarly, if we want to find the midpoint of a segment in the 3-dimensional space, we can determine the midpoint coordinate using the formula:

\((x,y,z) = [\frac{x_1+x_2}{2},\frac{y_1+y_2}{2},\frac{z_1+z_2}{2}]\)

Here in 3-D case coordinates of the point will be \((x_1,y_1,z_1) and (x_2,y_2,z_2)\)

Also in statistics and other areas of science, we have a similar kind of formula. Let us take the case for calculating the elasticity. We will use the average percentage change in both quantity as well as price. This is popularly known as the midpoint method for elasticity. It is represented by the following equations:

\(\displaystyle\text{percent change in quantity}=\frac{Q_2-  Q_1}{(Q_2+Q_1)\div{2}}\times{100}\)

i.e. \(\displaystyle\text{percent change in price}=\frac{P_2-P_1}{(P_2+P_1)\div{2}}\times{100}\)

Solved Examples

Example-1: Find the midpoint of a line whose endpoints are (4, 5) and (6, 7)?

Solution:

Given, \((x_1, y_1) = (4, 5)\)

And \((x_2, y_2) = (6, 7)\)

According to the formula we can have the midpoint (x, y) as follows:

\((x,y) = [\frac{x_1+x_2}{2},\frac{y_1+y_2}{2}]\)

i.e. \((x,y) = [\frac{4+6}{2},\frac{5+7}{2}]\)

i.e. \((x,y) = (5, 6)\)

Example-2: How do you solve a problem such the point (0,2) is the midpoint of (2,-3) and what point?

Solution:

The first point is (2,-3).

Let us assume that another point’s coordinate is (m,n).

Now,

(x,y) = \([\frac{x_1+x_2}{2},\frac{y_1+y_2}{2}]\)

Putting known values, we get:

(0,2)= \([\frac{2+m}{2}, \frac -3+n{2}]\)

i.e.

\(\frac{2+m}{2} = 0\)

And \(\frac{-3+n}{2} = 2\)

Solving we get

m= -2

and n=7

Thus the second point will have coordinate (-2,7)