Properties of Parallelogram, Rhombus, Rectangle and Square

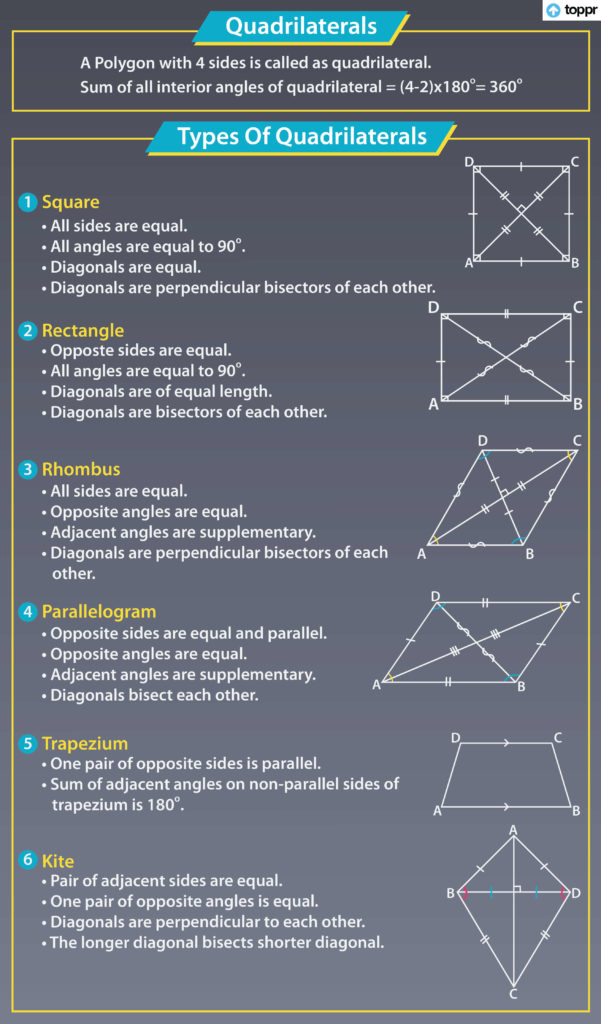
Quadrilaterals are closed figures with four sides. As they have four angles these are also referred to as quadrangles. A parallelogram is also a quadrilateral like the other common quadrilaterals rectangle and square. In this chapter, we shall learn the specific properties of parallelograms and rhombus.

Suggested Videos

 

Parallelogram

Parallelogram, as the name suggests, has a close association with parallel lines. Yes, this four-sided closed figure has parallel lines. In short, it is a closed figure with four sides with each pair of opposite sides parallel to each other.

In the figure above, all the shapes have parallel opposite sides, this means that all the closed figure shapes in the image above are parallelograms. Yes, a rectangle and square are also types of parallelograms which show properties peculiar to their names as well.

Properties of Parallelogram

A parallelogram has four sides and four angles. Sometimes the sides and angles may be equal while sometimes they may be different. The difference in sides and angles gives the final shape a different name. For example Square, rectangle, rhombus etc.

The figure above is of a parallelogram PQRS. What do you notice? PQ and RS are opposite sides and are parallel to each other. Another pair of opposite sides PS and QR are also parallel to each other. PQ and PS are adjacent sides, where PS starts when PQ ends.

These adjacent sides when intersecting with each other from adjacent angles. In the figure above ∠ P is adjacent to ∠S and ∠Q is adjacent to ∠R. ∠P is opposite to ∠R and is equal in measurement. In a parallelogram, two adjacent angles are supplementary while opposite angles are equal in measurement.

You can download Quadrilaterals Cheat Sheet by clicking on the download button below

Browse more Topics under Understanding Quadrilaterals

• Polygon and Its Types
• Angle Sum Property of Polygons
• Properties of Trapezium and Kite

Proofs

• In a parallelogram, opposite sides are equal in length: A parallelogram if bisected by a diagonal gives two triangles. In the figure, ∠1 = ∠2 and ∠3= ∠4 (opposite angles). SQ is the common line segment adjoining the triangles. Therefore using the ASA congruency we can state that Δ PQS and Δ QRS are congruent to each other. Hence from the above theory, we say that PQ=RS and PS=QR.

• The opposite angles of a parallelogram are equal in measurement. This property of a parallelogram is proved true using the ASA congruency condition in a parallelogram. When a parallelogram is divided into two triangles we get to see that the angles across the common side( here the diagonal) are equal. This proves that the opposite angles in a parallelogram are also equal.
• The adjacent angles are supplementary.
• The diagonals of a parallelogram are not of equal length. They bisect with each other at the point of intersection with equal sides across the point of intersection. This can be proved using the ASA criterion as well. When we divide the parallelogram through two diagonals, we see that four triangles are formed. With the help of ASA congruency criterion, we see that opposite triangles in a parallelogram are congruent to each other.

Rhombus

A rhombus is a special case of the kite. A kite has an adjacent pair of sides equal in measurement. Unlike a kite, a rhombus is a quadrilateral with all sides of equal length. A rhombus can also be called a type of parallelogram because its sides are parallel to each other.

• The sum of angles in a rhombus is 360°.
• Opposite angles are equal to each other and adjacent angles are supplementary angles.

Almost all the properties of Rhombus are like a parallelogram. How is Rhombus different then? The main point of difference is the diagonal of a rhombus. The diagonal of a rhombus bisect each other at 90°. This means that the diagonals of a Rhombus bisect each other perpendicularly.

In rhombus ABCD, sides AB=BC=CD=DA;
∠O = 90°
OB=OD and OC=OA.

Rectangle

A rectangle is a four-sided closed figure with each side making a right angle with another. A rectangle is also a parallelogram, the only difference lies in the angles constituting the figure. Like other parallelograms, opposite sides in a rectangle are parallel to each other. Its sides are generally called Lengths and Breadths.

When we measure the pair of sides we find that the parallel sides are equal in length as well. Since the angles in a rectangle are equal, a rectangle can be considered to be a parallelogram with equal angles.

Square

In a rectangle, only the opposite sides are of equal length, but in a square, all sides share equal length. We may also put it as a rectangle with all equal sides. The diagonals in a square show the following properties:

• They bisect one another
• The diagonals are of equal length
• All the diagonals are perpendicular to one another

From the discussion above we can now differentiate how different types of parallelograms show different properties.

Solved Examples for You

Question: Find the value of the following angles in the rhombus ABCD:

1. ∠XAB
2. ∠XCB and
3. ∠AXB

Solution:

a) DXB is the diagonal that bisects the ∠ABC
Since ∠ABX = 40 °, ∠ABC = 2× 40 = 80°
Now in a rhombus, the sum of adjacent angles is 180° so ∠ABC+∠BAD = 180°
80° + ∠BAD = 180°
∠BAD= 180-80=100°
∠BAD = 100°
∠BAD is bisected by diagonal,AXC, so ∠ XAB = 50 °

b) ∠XAB is opposite to ∠ XCB, therefore ∠XCB=50°

c) ∠AXB is formed by the diagonal that perpendicularly bisect each other, therefor ∠AXB is 90°.

Question: A parallelogram FAST is shown in the figure. Find the missing angles.

Solution: FAST is a parallelogram. Let us first recollect the angle related properties of a parallelogram.

• Opposite angles are equal.
• Adjacent angles are supplementary.

Using the first property, let us find the value of  ∠FAS
∠FAS is opposite to ∠FTS, so ∠FAS shall be 80°

Now let us use the 2nd angle property, which says adjacent angles are supplementary.
According to this property, ∠FAS + ∠AST = 180°
80° + ∠AST = 180°
∠AST = 180-80
= 100°

For finding the value of ∠AFT we need to use the opposite angle property.
∠AFT =∠AST
∠AST = 100°
So, ∠AFT = 100°

Question– What shape parallelograms have?

Answer- Parallelograms are shapes that are consisting of four sides with two pairs of sides that are parallel. The four shapes that we can say necessarily meet the requirements of a parallelogram are square, rectangle, rhombus, and rhomboid

Question- List any 4 properties of parallelograms.

Answer- The four properties of parallelograms are that firstly, opposite sides are congruent (AB = DC). Then, opposite angles are congruent (D = B). Moreover, if one angle is right then automatically all the other angles are right. Further, the diagonals of a parallelogram bisect each other. Most importantly, consecutive angles are supplementary (A + D = 180°).

Question- What makes a parallelogram a parallelogram?

Answer- A parallelogram is basically a flat shape. It has opposite sides parallel which is also equal in length. Thus, Angles ‘a’ and ‘b’ add up to 180°, so we refer to them as supplementary angles. Similarly, squares, rectangles and rhombuses fall in the same category of parallelograms.

Question- What are some examples of a parallelogram?

As it is clear by now that parallelograms have four sides, plus the sides opposite each other are parallel. In other words, they do not intersect with each other. Therefore, we see that square, rhombus, and rectangle all verify as examples of parallelograms.