Inverse Square Law Formula

In physics many laws observe the inverse square rule, one such law is the one governing intensity. Let us learn more about Inverse Square Law Formula in detail.

What is the Inverse Square Law Formula?

The intensity of the light to an observer from a source is inversely proportional to the square of the distance from the observer to the source. This shows that as the distance from a light source increases, the intensity of light is equal to a value multiplied by 1/d². Thus closer a light source brighter it is. This is very evident from the fact that in the night when a car approaches us from a distance it looks dark but as it comes near the light the headlights make it be brighter as the distance between the observer and the car has decreased.

Similar concepts are also used in the gravitational law and the electric charge law of the Coulomb’s law. The formula for this is shown below. The inverse square law of intensity is applicable to not only the visible rays in the electromagnetic spectrum but also to all the other spectrums like the gamma rays, X rays, UV rays etc.. The intensity of visible light is measured in candela units, while the intensity of other waves is measured in Watts per meter squared (W/m²).

The Formula:

The law states that the intensity of light from a given source varies inversely with the square of the distance of the source. In short, as the distance increases the intensity of the light from the source decreases. Mathematically, the formula can be written as,

I ∝ (1/d²)

Where the distance is d(metres), the intensity of the radiation is I(candela).

If the distances are d₁ and d₂ and the intensities are I₁ and I₂ respectively. Then Inverse-square law is  as follows,

I1/I2∝ d2²/d²1

Inverse square law formula is used in finding distance or intensity of any given radiation. The intensity is calculated in Lumen or candela and distance is given in meters. It has widespread applications in problems grounded on the light.

Solved Examples for Inverse Square Law Formula

Q: If a bright flashlight has a light intensity of 15.0 candela at a distance 1.00 m from the lens, what is the intensity of the flashlight 100.0 m from the lens?

Answer: The intensity at the farther distance can be found using the inverse square formula as follows,

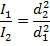
If d₁ = 1.00 m  distance from the lens, and d₂ = 100.0 m distance from the lens, then I₁ = 15.0 candela, and we need to find I₂.

Solving for  I₂ we get,

I₂  = 0.0015 candela.

Q: The intensity of the radio signal is 0.120 W/m² at a distance of 16.0 m from a transmitter. What is the intensity of the signal at a distance of 4.00 m from the same transmitter?

Answer: The intensity at the near distance can be found using the inverse square formula as follows,

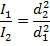
If d₁ = 4.00 m from the transmitter, and d₂ = 16.0 m from the transmitter, then

I₂ = 0.120 W/m², and we need to solve for I₁. This requires rearranging the equation:

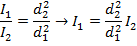
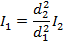 and substituting  the values that are known into the equation:

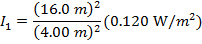
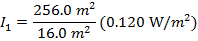
I₁ = (16.0)(0.120 W/m²)

I₁ = 1.92/m²

The intensity of the radio signal from the transmitter is 1.92 W/m².

Calculations which use inverse square law tend to be simple and hence they are used as a part of much larger calculations.