We know that a circle is a very important two-dimensional shape in geometry. Its perimeter is known as the circumference. There is a term “arc” is used with reference to the circle. It is any portion of the circumference of a circle of any length. The obviously maximum length of an arc will be equal to the length of the circumference of the circle. In this article, we will see the details about the arc and computation of the arc length formula with examples. Let us begin the topic!
Arc Length Formula
What is Arc and Arc Length?
An arc is any connected part of the circumference of the given circle. An arc length is a distance from one endpoint of the arc to the other. Thus to find an arc length we will require the knowledge a bit about the geometry of a circle.
Since the arc is a portion of the circumference of the circle and we also know that complete circumference is making 360 degrees angle at the center of the circle. So, by knowing the portion of the circumference i.e. arc and arc’s central angle we can easily find the length of the arc.
An angle is a geometrical figure when two lines meet at a common point on a plane. In a given circle, the length of the arc is a portion of the length of its circumference. The arc length will be the measure of the distance along the curved line making up the arc. It will be longer than the straight line distance between its endpoints which is known as a chord.
Arc Lenght Formula
For a given circle arc length, C can be computed as,
C = \(\frac{\theta }{180^{\circ}}\times \pi\times r\)
where,
| C | Arc Length |
| r | Radius of circle |
| \(\theta\) | Centre Angle by Arc in degrees |
| \(\pi\) | 3.14 |
Also if the centre angle is measured in radian then this angle should be converted into degree using the conversion formula as,
1 \(\; radian = \frac{180^{\circ}}{\pi}\)
where π = 3.14
Derivation of the Arc Lenght Formula
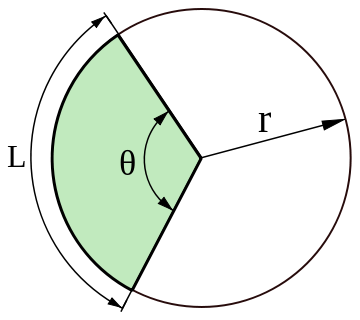
Angle made by circumference at the center of circle = \(360^{\circ}\)
And length of circumference = \(2\times \pi\times r\)
So angle \theta made by an arc with arc length c at the center will be,
\(\theta =\frac{360^{\circ}}{2\times \pi\times r}\times c\)
i.e. \(\theta =\frac{180^{\circ}}{\pi\times r}\times c\)
i.e. c = \(\frac{\Theta }{180^{\circ}}\times \pi\times r\)
Hence proved.
Solved Example
Q: If the circumference of a circle is 54 cm. In it an arc ABC is making the center angle \(120 ^ {\circ}\). Find out the arc length?
Solution:
It is given that circumference length = 54 cm.
First we will find the radius of the ccircle,
i.e. r = \(\frac{circumference\; length}{2\pi}\)
i.e. r = \(\frac{54 }{2\pi}\)
Also centre angle \(\theta = 120 ^{\circ}\)
Now, we know that arc length of circle using the arc length formula,
C = \(\frac{\theta }{180^{\circ}}\times \pi\times r\)
Now putting values of radius r and center angle \(\theta\) in the above formula we get,
C = \(\frac{120^{\circ}}{180^{\circ}}\times \pi \times r\)
Here we can simplify \pi from the numerator and denominator both.
Then,
C= \(\frac{2}{3}\times \frac{54}{2}\)
i.e. C = 18 cm.
Therefore the arc length will be 18 cm.
