Elementary Operations! Let’s get a deeper understanding of what they actually are and how are they useful. Elementary operations for matrices play a crucial role in finding the inverse or solving linear systems. They may also be used for other calculations. The matrix on which elementary operations can be performed is known as an elementary matrix.
Suggested Videos
What is an Elementary Matrix?
An elementary matrix is a matrix which differs from the identity matrix by one single elementary row operation (or column operation). Now, let’s consider a matrix given below,
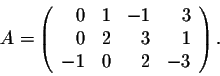
Its rows are
Its columns are
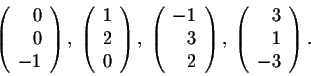
Let us consider the matrix transpose of A
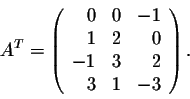
Its rows are
![]()
Browse more Topics under Matrices
- Matrix
- Types of Matrices
- Addition of Matrices
- Scalar Multiplication of Matrices
- Symmetric and Skew-Symmetric Matrices
- Multiplication of Matrices
- Transpose of a Matrix
- Invertible Matrices
Elementary Matrix Operations
- Interchange two rows or columns.
- Multiply a row or a column with a non-zero number.
- Add a row or a column to another one multiplied by a number.
1. The interchange of any two rows or two columns
Symbolically the interchange of the ith and jth rows is denoted by Ri ↔ Rj and interchange of the ith and jth column is denoted by Ci ↔ Cj. For example, applying R1 ↔ R2 to $$A=\begin{bmatrix} 3 & -4 & 5\\ 1 & 1 & 2\\4 & 5 & 7\end{bmatrix}$$ gives $$A=\begin{bmatrix} 1 & 1 & 2\\3 & -4 & 5\\4 & 5 & 7\end{bmatrix}$$
2. The multiplication of the elements of any row or column by a non zero number
Symbolically, the multiplication of each element of the ith row by k, where k ≠ 0 is denoted by Ri → kRi. For example, applying R1 → 1 /2 R1 to $$A=\begin{bmatrix} 1 & 1 & 2\\ 3 & -4 & 5\\4 & 5 & 7\end{bmatrix}$$ gives $$A=\begin{bmatrix} 1/2 & 1/2 & 1\\3 & -4 & 5\\4 & 5 & 7\end{bmatrix}$$
3. The addition of the elements of any row or column, the corresponding elements of any other row or column multiplied by any non zero number.
Symbolically, the addition of the elements of the ith row, the corresponding elements of jth row multiplied by k is denoted by Ri → Ri + kRj. For example, applying R2 → R2 –2 R1, to $$A=\begin{bmatrix} 1 & 1 & 2\\ 3 & -4 & 5\\4 & 5 & 7\end{bmatrix}$$ gives $$A=\begin{bmatrix} 1 & 1 & 2\\1 & -6 & 1\\4 & 5 & 7\end{bmatrix}$$
Row Equivalence
Two matrices are row equivalent if and only if one may be obtained from the other one via elementary row operations. For example, show that the two matrices are row equivalent.
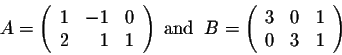
Answer: We start with A. If we keep the second row and add the first to the second, we get
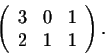
We keep the first row. Then we subtract the first row from the second one multiplied by 3. Hence, we get
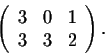
We keep the first row and subtract the first row from the second one. Hence, we get
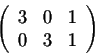
[source: sosmath]
which is the matrix B. Therefore A and B are row equivalent. The column equivalence also implies the same rule.
Solved Examples For You
Question 1: If you switch the first row with the fourth row, what will the new first row be?
$$A=\begin{bmatrix} 3 & 4 & 2 & 11\\9 & 1 & 0 & 0\\0 & 1 & 0 & 2\\0 & 0 & 6 & 1\end{bmatrix}$$
- 3, 4, 2, 11
- 9, 1, 0, 0
- 0, 1, 0, 2
- 0, 0, 6, 1
Answer : Option (D) 0, 0, 6, 1
Question 2: $$A=\begin{bmatrix} 1 & 2 & 3\\4 & 5 & 6\\7 & 8 & 9\end{bmatrix}$$
B is matrix obtained by subtracting 4 times 1st rowfrom 2nd row of A. C is matrix obtained by subtracting 7 times 1st row from 3rd row, then C is
- $$\begin{bmatrix} 1 & 2 & 3\\0 & -3 & -6\\0 & -3 & -12\end{bmatrix}$$
- $$\begin{bmatrix} 1 & 2 & 3\\0 & 1 & 2\\3 & 4 & 5\end{bmatrix}$$
- neither (A) nor (B)
- cannot be calculated
Answer : Option (A)
$$C=\begin{bmatrix} 1 & 2 & 3\\0 & -3 & -6\\0 & -3 & -12\end{bmatrix}$$
Question 3: Define the elementary operation?
Answer: The elementary operations are generally the operations in the elementary arithmetic. These are; the addition, multiplication, subtraction, and division. Moreover, the elementary row operations or the elementary column operations.
Question 4: What is the elementary row operation on a matrix?
Answer: The ‘basic operation’ on the numerical values and inputs is the addition, subtraction, multiplication, and division. For matrix, there are 3 basic row operations, this means there are 3 techniques that we can do with the rows of the matrix.
Question 5: What is the rank when it comes to a matrix?
Answer: The rank of a matrix refers to (A) ‘the highest possible number of the linearly independent column vectors in a matrix’ or (B) that says ‘the greatest possible number of the linearly self-determining row vectors in a matrix.
Question 6: What is the product of an elementary matrix?
Answer: An elementary matrix basically refers to a matrix that we can achieve from the identity matrix by a single elementary row operation. On multiplying the matrix ‘A’ by the elementary matrix ‘E’ it results in ‘A’ to go through the elementary row operation symbolized by ‘E’.








MATHEMATICS WAS TOO DIFFICULT FOR ME BUT WHEN I LEARN FROM TOPPR I FEEL MATHEMATICS IS TOO EASY I LIKE IT