Monopoly Market

The term Monopoly means ‘alone to sell’. In a monopoly market, there is a single seller of a particular product with no strong competition from any other seller. In this article, we will look at the features of a monopoly market.

Features of a Monopoly Market

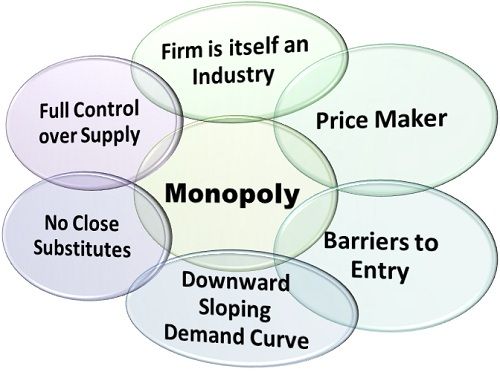
1. Single Seller of the Product

In a monopoly market, usually, there is a single firm which produces and/or supplies a particular product/ commodity. It is fair to say that such a firm constitutes the entire industry. Also, there is no distinction between the firm and the industry.

Browse more Topics under Determination Of Prices

• Intro to Determination of Prices
• Changes in Demand
• Changes in Supply
• Simultaneous changes in Demand and Supply
• Features of Perfect Competition
• Price Determination under Perfect Competition
• Long Run Equilibrium of Competitive Firm and Industry
• Monopolist’s Revenue Curve
• Price Discrimination
• Monopolistic Competition
• Oligopoly
• Kinked Demand Curve

2. Entry Restrictions

Another feature of a monopoly market is restrictions of entry. These restrictions can be of any form like economical, legal, institutional, artificial, etc.

3. No Close Substitutes

Usually, a monopolist sells a product which does not have any close substitutes. Therefore, the cross elasticity of demand for such a product is either zero or very small. Also, the price elasticity of demand for the monopolist’s product is less than one. Hence, in the monopoly market, the monopolist faces a downward sloping demand curve.

Now, to a certain extent, all goods are substitutes for one another. However, certain essential characteristics in a commodity or a group of commodities can lead to gaps in this chain of substitution.

A monopolist or a single seller is one who identifies these gaps, excludes the competition, and controls the supply of a particular commodity. Such a monopolist can use his single-selling power in any manner to realize maximum revenue. This includes price discrimination.

It is important to note that in real life, complete monopoly is extremely rare. However, one firm can dominate the supply of a good or a group of goods. For example, in public utilities, like transport, water, electricity, etc., monopolistic markets usually exist to reap the benefits of large-scale production.

4. Price Maker

Since there is only one firm selling the product, it becomes the price maker for the whole industry. The consumers have to accept the price set by the firm as there are no other sellers or close substitutes.

Solved Question on Monopoly Market

Q: All of the following are characteristics of a monopoly except:

1. there is a single firm.
2. the firm is a price taker.
3. the firm produces a unique product.
4. the existence of some advertising.

Answer: According to the features of a monopoly market, there is a single seller with no close substitutes for the commodity in the market. Therefore, options a and c are characteristics of a monopoly. Further, a monopolist will try to get more buyers by advertising his goods. Hence, option d is also applicable to a monopoly market. Finally, in a monopoly, the seller can use his monopolistic powers to realize maximum revenue, Hence, he is not a price-taker. Therefore, option b is the correct answer since it is not applicable to a monopoly.