Welcome. In this discussion, we will be looking at an important concept used in limits and calculus. We will discuss the concept of the Sandwich theorem. This theorem is quite simple to understand and has a lot of applications in calculus. It is used especially while using trigonometric functions.
A clear understanding of sandwich theorem will prove beneficial not just in calculus but in other concepts like binomial theorem as well. Students are expected to reach out to faculties in case of any doubts they may encounter while learning such concepts.
Suggested Videos
Sandwich Theorem
The sandwich theorem is also known as Squeeze theorem or Pinch theorem. This is used to extrapolate the value of a function at a point x by using two functions in the neighbourhood. There is also an interesting anecdote associated with the sandwich theorem.
It states that there are 2 policemen escorting a drunk. Both these policemen enter a cell, then, regardless of the fact that the drunk is wobbling, he must enter the cell too. This is exactly the way this theorem is used. Let us look at its statement.
Browse more Topics under Limits And Derivatives
- Limits
- Direct Method
- Derivatives
- First Principle of Differentiation
- Algebra of Derivative of Functions
- Standard Simplifications
Let f, g and h be three functions having the same domain such that f(x) ≤ g(x) ≤ h(x). For a real number ‘a’ if lim x->a f(x) = lim x->a h(x) = l, then lim x->a g(x) must be equal to l.
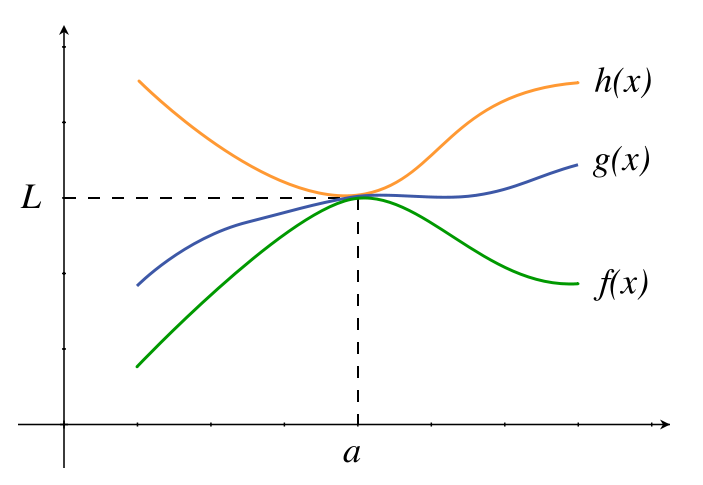
This is illustrated in the above diagram. Let us look at the proof using an example.
Prove that cosx < sinx / x <1
Proof:

In the above figure, we see Δ ABE, Δ ADF, Δ ADB and sector ADB.
Now, AB = AD (isosceles traingle)
Area (ΔABD) < Area (sector ADB) < Area (ΔADF)
1/2.AD.EB < x/2π.π.AD2 < 1/2.AD.DF
Cancelling the common terms from all sides, we get
EB < x.AD < DF
From Δ ABE, sinA = EB/AB, so EB = AB sinx (angle A= angle X)
Also, tanA = DF/AD, so DF = ADtanX
But AB = AD and
tanA = sinX/CosX
so, AD.sinA < x.AD < AD.sinA / cosA
= 1 < x / sinX < 1 / cosX
Taking reciprocals we get,
cosx < sinx / x < 1
Hence proved.
Using the above theorem we can easily prove some other trigonometric identities such as
- limx->0sinx/x =1
- limx->0 (1 – cosx)/x =0
We have to keep in mind some points while evaluating the limits.Suppose while evaluating a function where limx->af(x)/g(x) exists such that f(x) = 0 and G(x) = 0. Then in such cases, we rewrite f(x) and G(x) in such ways that we get 2 functions. This can be said as f(x) = f'(x).f”(x) such that f'(x) = 0.
Similarly we get g(x)=g'(x).g”(x) such that g'(x)=0. We then cancel out the common terms and we get the new limits as
limx->af(x) / g(x) = f'(a)/g'(a)
Solved Example for You
Question 1: Evaluate lim x->0 tanx / x
Answer : = lim x->0 sinx / x.cosx
= lim x->0 sinx / x . limx->0 1 / cosx
= 1.1 = 1
Question 2: What is a sandwich theorem in limits?
Answer:In this theorem, iff(x) ≤ g(x) ≤ h(x) for all numbers, and at some point x = k then we have f(k) = h(k), then g(k) must also be equal to them. In addition, we can use this theorem to find tricky limits like sin(x)/ x at x = 0, by squeezing sin(x)/x amid two nicer functions and using them to find the limit at x = 0.
Question 3: What makes a function continuous?
Answer: The function f is continuous at a point x = a. Moreover, when first, the function f is defined at a. Second the limit of f as x approaches a from the right-hand and left-hand limits exist and re equal, and lastly, the limit of f as x approaches is equal to f(a).
Question 4: What is jump discontinuity?
Answer: It happens when the two-sided limit exists, still isn’t equal to the function’s value. Moreover, it is when the two-sided limit doesn’t exist because the one-sided limits aren’t equal.
Question 5: Why we need a sandwich theorem?
Answer: We use it in calculus and mathematical analysis. Normally, we use it to check the maximum of a function via comparison with two other functions whose limits are known or easily computed.






Leave a Reply