Derivatives

So, the ‘derivative’ goes to a bar. What is his favorite pickup line? He says, “I like pushing things to their limits“. Well, that is the concept of derivatives for you. We will look into what lies beyond in this discussion. So, let us begin. But first a revision of the basics.

Suggested Videos

 

Introduction

The concept of a derivative is derived from the development of the concept of limits. As we know, the limit for a function f(x) at a point ‘a’ is the value that the function f(x) tends to achieve at point ‘a’ if it exists. Basically, with limits, we tend to define a function’s domain i.e. the reason in which the functional results can be obtained.

We have seen domains of various functions, for example, the domain of the function sinx is (-1, 1). This is where we introduce the concept of Derivative.

Derivative

Assume a function f(x) within its domain. Let us say, this function involves the calculation of the rate of change of velocity or as we know it the acceleration of a vehicle as it moves from one point to the other.

Now obviously the rate of change of velocity is instantaneous as the function is dependent on both the speed as well as the direction of the vehicle. If we are to find the instantaneous acceleration of the vehicle we will need the limits of the function at that instant.

A function denoting the rate of change of another function is called as a derivative of that function. In other words, a derivative is used to define the rate of change of a function.

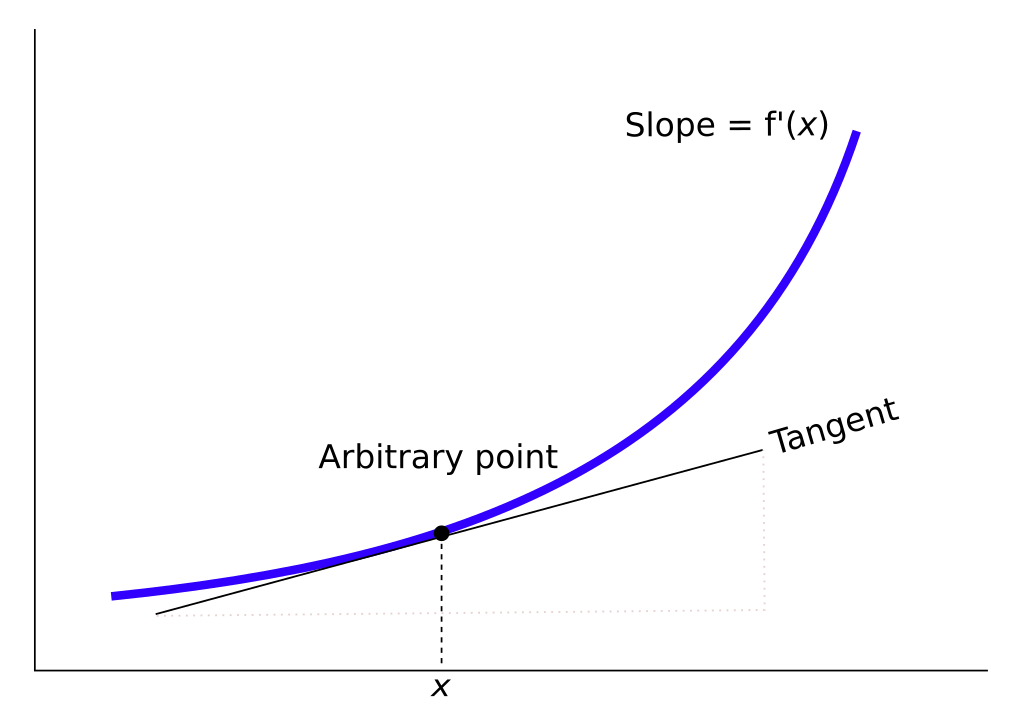
The most common example is calculating the slope of a line. As we know to calculate the slope of any point on the line we draw a tangent to it and calculate the value of tan of the angle it makes with the base. The derivative of a function f(x) at any point ‘a’ in its domain is given by:

lim_h->0 [f(a+h) – f(a)]/h

if it exists. It is denoted by f'(a) and f'(a) changes as the value of x changes in its domain. We have thus looked into and discussed clearly the concept of derivatives. We have derived its origins from the concept of limits and studied how the derivative is a rate of change of values in the domain defined.

The concept of limits and derivative is very important and forms the base of calculus. Students are expected to have a clear understanding of these concepts so as to enable them to effectively utilize them in the future.

Solved Examples for You

Question 1: Find the derivative of the function 2x²+3x-5 at x=1?

Answer: The derivative of a function f(x) at a point is given by:

f ‘(x) = lim _{h -> 0} [f(x+h) – f(x)]/h

Put in the above function we get:

f’ (x=1) = lim _{h -> 0} [(2(1+h)²+3( 1+h)-5)-(2+3-5)]/h

= lim _{h -> 0} [(2h²-h)]/h

= lim _h->0 {2h – 1} = -1

Question 2: What exactly is derivative?

Answer: The derivative is what measures the steepness of the graph of a function at a specific point on the graph. Therefore, we see that derivative is a slope.

Question 3: How are derivatives used in real life?

Answer: We make use of derivatives in real life to calculate the profit and loss in business by making use of graphs. Moreover, we use them to determine the speed or distance which we cover in miles per hour or km per hour and more. Similarly, they also have use in Physics for deriving equations.

Question 4: What is the difference between differentiation and derivative?

Answer: Basically, differentiation is the method of finding a derivative. The derivative of a function means the rate of change of the output value with regards to its input value. On the other hand, differential means the actual change of the function.

Question 5: What is a derivative function?

Answer: We use derivative in maths to show the rate of change which is the amount a function takes at a given point. In regards to functions acting on real numbers, it’s the slope of the tangent line at a point on a graph.