Thunderstorms, lightning, cyclones, and earthquakes are few natural phenomena that can cause a large-scale destruction of life and property. We can predict them to a certain extent but not perfectly. While lightning can be explained by using the concept of production of electric charge by rubbing, earthquakes are caused by a disturbance deep inside the earth’s crust. Let’s try to understand lightning and earthquakes a little better.
Suggested Videos
Lightning
When a thunderstorm develops, the air currents move upward whereas the water droplets move downward (remember last year’s syllabus). This movement also causes a separation of positive and negative charges on the clouds. The negative charges accumulate near the lower end of the cloud while the positive charges collect near the upper edge. Also, positive charge accumulates on the ground as well.

As these charges accumulate, it reaches a stage where it is impossible for air (a poor conductor of electricity) to resist the attraction between the positive and negative charges. When these charges meet, they create streaks of light and loud sounds. The charge gets discharged. This discharge can occur between two clouds or between clouds and earth. This causes lightning.
Browse more Topics under Some Natural Phenomena
Some Dos and Don’ts during a Thunderstorm or Lightning
Chances are that you will be caught in a lightning storm at least once in your life. Well, the following points might save your life:
- Try and find a safe place like a house or a building during a thunderstorm
- If you are outside, then try to avoid open places like fields or elevated places. Stay away from trees, poles and any metallic objects. Squat on the ground with your head between your knees.
- If you are inside your house or a building, then avoid using any electrical appliances or using running water (since water is a good conductor of electricity).
Many buildings have a Lightning Conductor installed to protect the building from a lightning strike. It is simply a metallic rod, taller than the building, which is inserted in the walls of the building with one end in the air and the other deep in the ground. In case of a lightning strike, the discharge happens through this rod and saves the building from its effects.
Earthquakes
Earthquake is the sudden shaking or trembling of the earth for a short time caused by disturbance deep inside the earth’s crust. Have you ever wondered what causes earthquakes? Let’s understand the structure of earth before looking at the reasons behind earthquakes. Internally, the earth is made up of four layers, the crust, mantle, outer core and inner core.
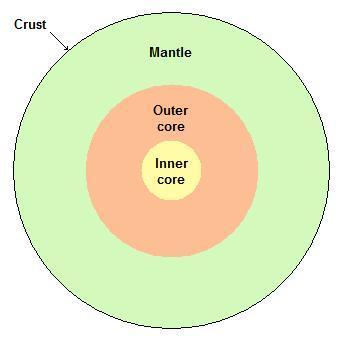
Source: Wikipedia
The Crust is not a single piece covering the inner layers. It is fragmented into smaller plates. These plates are in continuous motion. Every time they collide with each other or go above/ below the other, a disturbance is felt in the crust. This is an Earthquake.

However, we are yet to understand how and when these plates collide or brush against one another. Hence, predicting an earthquake is currently not possible. Sometimes, we also experience earthquakes after a volcanic eruption or an underground nuclear explosion.
The areas where these plates meet are more prone to an earthquake than the others. These weak zones are called the Seismic or Fault Zones. The Earthquake zones in India are as follows:

Source: Wikipedia
The magnitude of an earthquake is measured on the Richter scale. The scale is based on the amount of loss to life and property that an earthquake can cause. The higher the magnitude of an earthquake on this scale, the more destruction it can cause. Scientists have also devised an instrument called the Seismograph which records the waves produced by the tremors on the surface of the earth. This helps them estimate its power to cause destruction.
You can download Some Natural Phenomena Cheat Sheet by clicking on the download button below

Some precautions and tips to help during earthquakes
Since earthquakes cannot be predicted accurately, it better to be prepared for it especially for people living in the earthquake-prone zones. Here are some tips:
- Construct homes that are quake-resistant.
- Use timber and mud instead of cement and steel to keep damage minimum.
- Cupboards and shelves should be fixed to the wall.
- Reduce the number of hanging things in your house.
- Keep fire extinguishers handy at all times.
If you find yourself in the middle of an earthquake, here are some tips to follow:
- If you are outside, stay away from buildings, trees, and power lines. Stay close to the ground.
- If you are at home, sit under a strong table or bed. Stay away from objects that may fall in case the tremors increase.
Solved Questions For You:
Q: The weak zones around the boundaries of plates underneath Earth, which are prone to slide and cause earthquake are commonly known as:
A) Fault zone B) Erruption zone C) Explosive zone D) Sliding zone
Solution: A) As we saw, the surface of the earth is divided into various fractured plates. The boundaries of these plates are most prone to sliding and causing earthquakes. These regions are called the fault zones.






Leave a Reply