The determinant of a matrix is a number that is specially defined only for square matrices. Determinants are mathematical objects that are very useful in the analysis and solution of systems of linear equations. Determinants also have wide applications in engineering, science, economics and social science as well. Let’s now study about the determinant of a matrix.
Suggested Videos
The Determinant of a Matrix
To every square matrix A = [aij] of order n, we can associate a number (real or complex) called determinant of the square matrix A, where a = (i, j)th element of A. This may be thought of as a function which associates each square matrix with a unique number (real or complex).
If M is the set of square matrices, K is the set of numbers (real or complex) and f : M → K is defined by f (A) = k, where A ∈ M and k ∈ K, then f (A) is called the determinant of A. It is also denoted by | A | or det A or Δ.
$$ If A =\begin{bmatrix} a & b \\ c & d \end{bmatrix}, then \ determinant \ of \ A \ is \ written \ as \ |A| \ =\begin{vmatrix} a & b \\ c & d \end{vmatrix} = det A $$
You can download the FULL Determinants Cheat Sheet by clicking on the download button below
Browse more Topics under Determinants
- Properties of Determinants
- Minors and Cofactors of Determinant
- Area of a Triangle Using Determinants
- Adjoint and Inverse of a Matrix
- Solution of System of Linear Equations using Inverse of a Matrix
Learn Properties of Determinants here.
For a 1×1 Matrix
Let A = [a] be the matrix of order 1, then determinant of A is defined to be equal to a.
For a 2×2 Matrix
For a 2×2 matrix (2 rows and 2 columns):
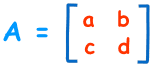
[source: mathisfun]
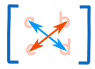
The determinant is: |A| = ad − bc or the determinant of A equals a × d minus b × c. It is easy to remember when you think of a cross, where blue is positive that goes diagonally from left to right and red is negative that goes diagonally from right to left.
[source: mathisfun]
Example: $$ If A =\begin{bmatrix} 2 & 3 \\ 4 & 8 \end{bmatrix}$$
|A| = 2 x 8 – 4 x 3
= 16 – 12
= 4
For a 3×3 Matrix
For a 3×3 matrix (3 rows and 3 columns):
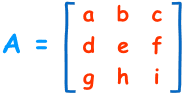
[source: mathisfun]
The determinant is: |A| = a (ei − fh) − b (di − fg) + c (dh − eg). The determinant of A equals ‘a times e x i minus f x h minus b times d x i minus f x g plus c times d x h minus e x g’. It may look complicated, but if you carefully observe the pattern its really easy!
[source: mathisfun]
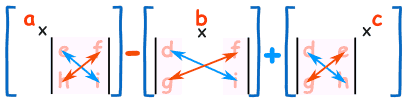
To work out the determinant of a matrix 3×3:
- Multiply ‘a’ by the determinant of the 2×2 matrix that is not in a’s row or column.
- Likewise for ‘b’ and for ‘c’
- Sum them up, but remember the minus in front of the b
As a formula (remember the vertical bars || mean “determinant of”):
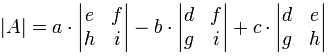
[source: mathisfun]
The determinant of A equals ‘a’ times the determinant of e × i minus f × h minus ‘b’ times the determinant of d × i minus f × g plus ‘c’ times the determinant of d × h minus e × g.
For 4×4 Matrices and Higher
The pattern continues for the determinant of a matrix 4×4:
- plus a times the determinant of the matrix that is not in a’s row or column,
- minus b times the determinant of the matrix that is not in b’s row or column,
- plus c times the determinant of the matrix that is not in c’s row or column,
- minus d times the determinant of the matrix that is not in d’s row or column,

[source: mathisfun]
As a formula:
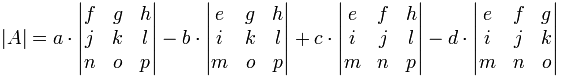
[source: mathisfun]
Notice the +−+− pattern (+a… −b… +c… −d…).
Study Adjoint and Inverse of a Matrix here.
Solved Examples For You
Question 1:$$ If \ f(x) =\begin{vmatrix} x & λ \\ 2λ & x \end{vmatrix},$$ then f(λx) – f(x) is equal to:
- x (λ2 – 1)
- 2λ (x2 – 1)
- λ2(x2 – 1)
- x2 (λ2 – 1)
Answer : $$ Given \ f(x) =\begin{vmatrix} x & λ \\ 2λ & x \end{vmatrix}$$
⇒ f(x) = x2 − 2λ2
Therefore, f(λx) − f(x) = (λx)2 − 2λ2 − (x2−2λ2)
=λ2x2−2λ2−x2+2λ2
=x2(λ2−1)
So, option D is correct.
Question 2: $$ If A =\begin{vmatrix} 0 & c & -b \\ -c & 0 & a \\ b & -a & 0 \end{vmatrix},$$ then (a2 + b2 – c2) |A| =
- abc
- a + b + c
- a3 + b3 + c3
- 0
Answer : |A| = 0 × (a2) −c(−ab) − b(ac) = 0 + abc – abc = 0
Question 3: What is the use of determinant of a matrix?
Answer: They are useful for solving linear equations, capturing how linear transformation changes volume or area, and changing variables in integrals. Furthermore, we can view determinant as a function whose input is a square matrix and whose output is a number.
Question 4: Can a determinant be negative?
Answer: Generally, a determinant is a real number and it is not a matrix. But, a determinant can be a negative number. Most importantly, it is not linked with absolute value at all except that they both use vertical lines.
Question 5: What if the determinant is 0?
Answer: In general perspective, if the determinant of a square matrix n × n A is zero then A is not invertible. Besides, if the determinant of a matrix is non-zero, the linear system it represents is linearly independent. However, when a determinant of a matrix is zero, its rows are linearly dependent vectors, and its columns are linearly dependent vectors.
Question 6: What is the use of Cramer’s rule?
Answer: It refers to a method that uses determinants to solve systems of equations that have the same number of equations as variables. In addition, it considers a system of two linear equations in two variables.








Is determinant available just for square matrix?
you mean if the determinant os non zero