In contrast to the concept of addition, the concept of resolution of vectors could be well understood. For say, in the process of addition, let’s consider \(\vec{a}\) and \(\vec{b}\) are directly added to get \(\vec{S}\). Now, let \(\vec{S}\) be broken down to obtain \(\vec{a}\) and \(\vec{b}\) back. This is referred to as the process of resolution. Let us study the chapter resolution of vectors and vector addition in detail.
Suggested Videos
Resolution of Vectors
A vector can be resolved into many different vectors, for resolution of vectors. For Example: Let us consider two numbers, say, 4 and 6, which is further added to obtain 10. Further, now 10 is broken or resolved. However, the number 10 can also be resolved into many other numbers like –10 = 5 + 5; 10 = 3 + 7 etc.
In a similar way, a vector can essentially be further broken or resolved to obtain multiple vectors of different magnitudes and directions. In Physics, vectors would be mainly resolved only along the coordinate axes, X, Y, and Z.
Browse more Topics under Motion In A Plane
- Introduction to Motion in a Plane
- Scalars and Vectors
- Addition and Subtraction of Vectors – Graphical Method
- Relative Velocity in Two Dimensions
- Uniform Circular Motion
- Projectile Motion
You can download Motion in a Plane Cheat Sheet by clicking on the download button below

Resolving Vectors along X and Y Axis
To resolve a vector on an X-Y plane, first, draw the vector. Then, label and create the constructions on the figure as mentioned below :
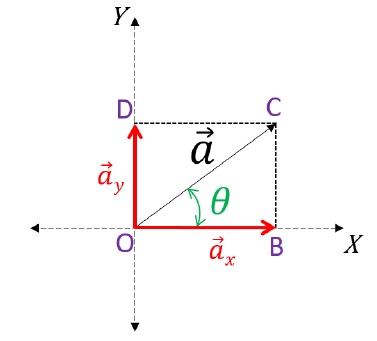
The complete figure seems to be like a parallelogram, further applying the Parallelogram law of vector addition. Herein, the two vectors \(\vec{a}_x\) and \(\vec{a}_y\) appears to be added by the parallelogram law of vector addition to obtain \(\vec{a}\). Therefore, with this, we can say that \(\vec{a}_x\) and \(\vec{a}_y\) are the resolved output of \(\vec{a}\) as \(\vec{a}\) has been again broken back to its components. Here,
- \(\vec{a}_x\) is the x-component; and
- \(\vec{a}_y\) is the y-component of \(\vec{a}\).
In order to find the magnitudes of each component, in △OBC:
cos θ = OBOC
Therefore, OB = OC cos θ
Hence, |\(\vec{a}_x\)| = |\(\vec{a}\)| cos θ [ Magnitude of x – component ]
sin θ = BCOC
So, BC = OC sin θ;
Also, BC = OD ( Opposite sides of Rectangle );
Therefore, |\(\vec{a}_y\)| = |\(\vec{a}\)| sin θ [ Magnitude of y – component ]
Note
The General Rule of Thumb states that the subtended angle will always touch one of the components. Further, the component which the given angle touches or the given angle is subtended with will be the cos component of the given vector. Whereas the other will automatically be the sin component.
Unit Vectors along Co-ordinate Axes
For the co-ordinate axes, there are special unit vectors designated by convention î, ĵ, and k̂, which respectively represents X, Y, and Z axes. By the property of unit vectors, |î| = |ĵ| = |k̂| = 1
Writing Vectors in Component Form: Using Coordinate Axes Unit Vectors
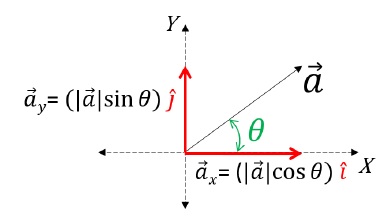
A vector can be expressed as a product of its magnitude and direction. Therefore,
- \(\vec{a}_x\) = |\(\vec{a}\)| cos θ î. The magnitude of \(\vec{a}_x\), which is |\(\vec{a}_x\)|, is multiplied to the direction in which \(\vec{a}_x\) lies, which is the direction of x-axis, represented by the unit vector î.
- \(\vec{a}_y\) = |\(\vec{a}\)| sin θ ĵ. The magnitude of \(\vec{a}_y\), which is |\(\vec{a}_y\)|, is multiplied to the direction in which|\(\vec{a}_y\)| lies, which is the direction of y-axis, represented by the unit vector ĵ.
- Now we know that \(\vec{a}\) = \(\vec{a}_x\) + \(\vec{a}_y\).
Therefore, \(\vec{a}\) = (|\(\vec{a}\)| cos θ ) î + (|\(\vec{a}\)| sin θ ) ĵ.
Addition of Vectors and Subtraction of Vectors in Component Form (Expressed as Unit Vectors)
Consider the following figure:
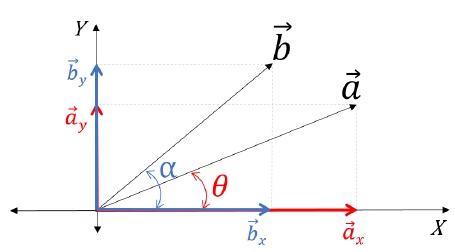
Expressing \(\vec{a}\) in component form,
- \(\vec{a}\) = \(\vec{a}_x\) + \(\vec{a}_y\);
- \(\vec{a}\) = |\(\vec{a}_x\)| î + |\(\vec{a}_y\)| ĵ;
- \(\vec{a}\) = (|\(\vec{a}\)| cos θ ) î + (|\(\vec{a}\)| sin θ ) ĵ
Expressing \(\vec{b}\) in component form,
- \(\vec{b}\) = \(\vec{b}_x\) + \(\vec{b}_y\);
- \(\vec{b}\) = |\(\vec{b}_x\)| î + |\(\vec{b}_y\)| ĵ;
- \(\vec{b}\) = (|\(\vec{b}\)| cos α ) î + (|\(\vec{b}\)| sin α ) ĵ
Operation, (\vec{S}\) = \(\vec{a}\) + \(\vec{b}\);
- \(\vec{S}\) = \(\vec{a}\) + \(\vec{b}\) = (|ax| î + |ay| ĵ) + (|bx| î + |by| ĵ);
- This implies, \(\vec{S}\) = (|ax| + |bx|) î + (|ay| + |by|) ĵ;
- Hence, \(\vec{S}\) = (|a| cos θ + |b| cos α) î + (|a| sin θ + |b| sin α) ĵ [Final Sum]
Operation, \(\vec{S}\) = \(\vec{a}\) – \(\vec{b}\);
- \(\vec{S}\) = \(\vec{a}\) – \(\vec{b}\) = (|ax| î – |ay| ĵ) + (|bx| î – |by| ĵ);
- This implies, \(\vec{S}\) = (|ax| – |bx|) î + (|ay| – |by|) ĵ;
- Hence, \(\vec{S}\) = (|a| cos θ – |b| cos α) î + (|a| sin θ – |b| sin α) ĵ [Final Difference]
Solved Examples for You
Example: A laser beam is aimed 15.95° above the horizontal at a mirror 11,648 m away. It glances off the mirror and continues for an additional 8570. m at 11.44° above the horizon until it hits its target. What is the resultant displacement of the beam to the target?
Solution: Let us break up the vector into their components –
| x1 = | r1 cos θ1 |
| x1 = | (11,648 m)cos(15.95°) |
| x1 = | 11,200 m |
| y1 = | r1 sin θ1 |
| y1 = | (11,648 m)sin(15.95°) |
| y1 = | 3,200 m |
| x2 = | r2 cos θ2 |
| x2 = | (8,570 m)cos(11.44°) |
| x2 = | 8,400 m |
| y2 = | r2 sin θ2 |
| y2 = | (8,570 m)sin(11.44°) |
| y2 = | 1,700 m |
Add vectors in the same direction with “ordinary” addition. –
| x = | 11,200 m + 8,400 m |
| x = | 19,600 m |
| y = | 3,200 m + 1,700 m |
| y = | 4,900 m |
Add vectors at right angles with a combination of pythagorean theorem for magnitude…
| r = | √(x2 + y2) |
| r = | √[(19,600 m)2 + (4,900 m)2] |
| r = | 20,200 m |
and tangent for direction.
| tan θ = | y | = | 4,900 m | |
| x | 19,600 m | |||
| θ = | 14.04° | |||







which situation we use vectors subtraction?
What are there applications in real life?