Linear Symmetry

We see different patterns in our daily life. Some seem similar some are quite different, but there come many instances where we see a pattern in perfect symmetry with the other. This is where the concept of symmetry is introduced to us. In the chapter below we shall deal with linear symmetry in regards to patterns.

Suggested Videos

 

Symmetry of Patterns

Before heading towards symmetry we need to first understand the term pattern. The pattern can be defined as any picture that follows a specific arrangement of designs and decorations. It can also be referred as a drawing which follows a definite design that might be or might not be repetitive. You can make a pattern yourself, let’s see how?

Take a paper and pour a few drops of ink on it. Fold the paper exactly at the center of the place where the ink has been poured. What do you observe? The drops of ink have taken a very unexpected shape. This shape can be termed as a pattern of ink on paper. Repeat the same a few more times. You will notice that the patterns made are very rarely repetitive. When a design or arrangement repeats it is said to follow a certain pattern of repetition.

Now, let us talk of symmetry. A design or thing is said to be in symmetry if it is in equality with its other counterpart. Symmetry in simple words means ‘same’. So, if a design is symmetrical then it has to follow the basic principle of symmetry like forming mirror halves when sliced from middle through a line.

Linear Symmetry

Have you seen objects which, when cut into half form identical parts? When an object is cut exactly in the middle, to form two identical parts, then the first is said to be symmetrical to the other. Likewise when we draw a line segment exactly in the middle of a pattern or drawing, if one part is identical to the other then the pattern is said to be linearly symmetrical.

(Source: Wikipedia)

Activity Time

Let us do an activity to clear the concept. Draw a circle of radius 5cm on a paper. At the diameter of the circle, draw a line segment cutting the circle into two halves. Fold the paper, what do you notice? The semi-circles when placed on each other lay exactly on each other perfectly.

This shows that the circle is linearly symmetrical to each other. Now, take an alphabet H and draw a line passing exactly from the middle of the alphabet. You will see that both the halves are an exact replica of each other.

Now, draw a big P on the paper and draw a line exactly in the middle of the alphabet. What do you notice? The line segment does not divide the alphabet into identical halves. This means that P is not a linearly symmetrical alphabet. Name a few more alphabets that are linearly symmetrical.

In simpler words, Linear symmetry defines the system that shows the object or pattern is drawn or made in equal proportion with the requisite sides.

Line of Symmetry

The line passing through an alphabet, an object or a pattern dividing them into exact halves, identical to one another is the line of symmetry. The line of symmetry forms the basis of any object showing linear symmetry. Lines of symmetry may be of two types depending on its orientation:

Vertical Line of Symmetry

If the line passes through the pattern from top to bottom, hence dividing the pattern into identical halves, then such line is the vertical line of symmetry. It is a standing line that divides the pattern into their replicating halves.

Horizontal Line of Symmetry

If the line passes through the pattern from right to left, hence dividing the pattern into identical halves, then such line is the horizontal line of symmetry. It is a sweeping line that divides the pattern into their replicating halves.

Both vertical line and horizontal line of symmetry pass through the middle of an object or alphabet or pattern to form mirror halves, which when placed on each other covers the other part.

Symmetry is a common occurrence in many areas of mathematics and hence is studied using every aspect of similarity and identity. An object is symmetrical or not can be understood only after studying linear symmetry and this is what the chapter intends to do.

Solved Example for You

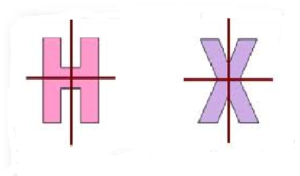
Question: Is the red line the line of symmetry in the following patterns:

Solution:

1. In the figure the red line divides the figure into mirror halves, it is, therefore, the line of symmetry.
2. The red line is not passing through the middle of the figure and thence does not divide the figure into exact halves replicating each other. The line is not the line of symmetry.
3. In the figure too, the line does not divide to form mirror halves hence cannot be called the line of symmetry.
4. Yes, the line is the line of symmetry because it is dividing the flower into replicating halves.