Basic Concepts of Vectors

While studying mathematics and sciences, we come across two types of quantities – scalars and vectors. The quantity that involves only value or magnitude is a Scalar quantity, like length, mass, speed, area, etc. On the other hand, the quantity that involves more than one values is a Vector quantity, like displacement, velocity, acceleration, force, weight, momentum, etc. In this article, we will look at the vector meaning by understanding the basic components of a vector.

Suggested Videos

 

Directed Lines

Look at the three images given below:

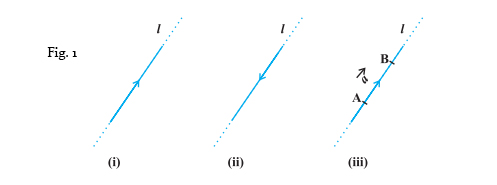
If ‘l’ is a straight line in a plane or three-dimensional space, then we can provide two directions to this line by using arrowheads. A line with an arrowhead is called a directed line. Fig. 1 (i) and (ii) are both directed lines. A point to note here: a directed line can go up to the end of the plane or the three-dimensional space.

We can also restrict a directed line to a line segment. In Fig. 1 (iii), you can see that we have restricted the line ‘l’ to the line segment AB. Hence, we have two values for the line ‘l’ – the direction of the line and the magnitude of the segment AB. So, we can say that a ‘directed line segment’ has magnitude as well as direction.

Browse more Topics under Vector Algebra

• Components of a Vector
• Types of Vectors
• Addition of Vectors
• Scalar (or Dot) Product of Two Vectors
• Vector (or Cross) Product of Two Vectors
• Section Formula
• Projection of a Vector on a Line

You can download Vector Algebra Cheat Sheet by clicking on the download button below

Definition 1

A quantity that has magnitude, as well as direction, is called a vector. From the figure above, the directed line segment shown in Fig. 1 (iii) is a vector. It is denoted as ‘vector  \( \vec{AB} \)’ or ‘vector \( \vec{a} \)’. The point A from where the vector \( \vec{AB} \) starts is called its initial point, and the point B where it ends is called its terminal point.

The distance between initial and terminal points of a vector is called the magnitude (or length) of the vector, denoted as |\( \vec{AB} \)|, or |\( \vec{a} \)|, or a. The arrow indicates the direction of the vector.

Note: Length is never negative. Hence, |\( \vec{a} \)| is always ≥ 0.

Position Vector Meaning

Now, look at the following diagram

Fig. 2 displays a right-handed rectangular coordinate system. Let’s consider a point ‘P’ in space, with coordinates (x, y, z) with respect to the origin O (0, 0, 0). The position vector of the point P with respect to the origin O is the vector \( \vec{OP} \), where O is the initial point and P is the terminal point of the vector.

Now, we already know about the distance formula. Applying it to find the magnitude of \( \vec{OP} \) or \( \vec{r} \), in this case, we get

|\( \vec{OP} \)| = \( \sqrt{x^2 + y^2 + z^2} \)

Also, in practice, the position vectors of points A, B, C, etc. with respect to the origin O are denoted by \( \vec{a} \), \( \vec{b} \), \( \vec{c} \), etc. as shown below.

Direction Cosines

Next, take a look at the figure below

Fig. 4 shows a position vector \( \vec{OP} \) (or \( \vec{r} \)) of a point P (x, y, z). The vector \( \vec{r} \) makes angles α, β, and γ with the positive directions of the x, y, and z-axes respectively. These are called direction angles. Now, the direction cosines of the vector \( \vec{r} \) are the cosine values of these angles. They are denoted as:

l = \( \cos{\alpha} \)
m = \( \cos{\beta} \)
n = \( \cos{\gamma} \)

Another thing that you may note from Fig. 4, is that the triangle OAP is a right-angled triangle. Hence, we have

\( \cos{\alpha} \) = \( \frac{x}{r} \)

where r stands for |\( \vec{r} \)|. Similarly, from the right-angled triangles OBP and OCP, we have

\( \cos{\beta} \) = \( \frac{y}{r} \) and \( \cos{\gamma} \) = \( \frac{z}{r} \)

Therefore, the coordinates of the point P can be expressed as (lr, mr, nr). These numbers, lr, mr and nr, are proportional to the direction cosines of the vector \( \vec{r} \). They are called direction ratios of the \( \vec{r} \) and are represented as a, b, and c respectively.

Solved Examples for You

Question 1: Classify the following measures as scalars and vectors.

1. 10 kg
2. 2 meters north-west
3. 40°
4. 40 watt
5. 10^-19 coulomb

Answer :

1. 10 kg is weight and has only magnitude and no direction. Hence, is is a Scalar.
2. 2 meters north-west has a magnitude of 2 meters and a direction, north-west. Hence it is a Vector.
3. 40ºis temperature and has only magnitude and no direction. Hence, is is a Scalar.
4. 40 watt is power and only has magnitude. It does not have any direction. Hence, is is a Scalar.
5. 10^-19 coulomb is an electric charge. It does not have direction and only has magnitude. It is a Scalar.

Question 2: how to define a vector?

Answer:Vector refers to an object that has both a direction and a magnitude. We can represent it as a fixed-line segment, whose length is the magnitude of the vector and with an arrow indicating the direction. In addition, the direction of the vector is from its tail to its head.

Question 3: What is the starting point of a vector?

Answer: We always represents a vector by an arrow when a line segment represents it. Furthermore, the starting point of a vector is known as the initial point and the endpoint is known as terminal point.

Question 4: Is the position a vector?

Answer: Yes, the position is a vector quantity because it has both magnitude (size) and direction. Moreover, the magnitude of a vector quantity is a number (with units) that tells you how much of the quantity there is, and the direction tells you which way it is pointing.

Question 5: what is a negative vector?

Answer: It is a vector that points in the direction opposite to the reference positive direction. In simple words, negative vectors have the opposite direction to the position positive direction. Moreover, a scalar vector can also be added or subtracted.