Electric Potential Energy and Electric Potential

Do you think charges are stationary or do they move from one place to another? They of course do. Otherwise, how would you get those electric shocks when you touch a live wire! This chapter of electricity is quite interesting and there is so much to learn. In this section, we will cover the concept of electric potential energy.

Suggested Videos

 

Electric Potential Energy

When you move around in the gravitational field of the earth, you have to make efforts. In other words, you have to work by exerting force if you want to change your position in a field. Electric charges have fields around them and thus a charge has to do work if it intends to change its position. This work is the electric energy or the electric potential energy of the charge.

We know that central forces are conservative in nature. This implies, the work done on any particle moving under its influence does not depend on the path taken by the particle but depends on initial and final positions of the particle. For conservative forces, work done on particle undergoing displacement can be expressed in terms of the potential energy function. Now, we will look at electric potential energy.

Browse more Topics under Electrostatic Potential And Capacitance

• Capacitors and Capacitance
• Electrostatics of Conductors
• The Parallel Plate Capacitor
• Energy Stored in a Capacitor
• Combination of Capacitors
• Dielectrics and Polarisation
• Effect of Dielectric on Capacitance
• Van De Graaff Generator

How to calculate electric potential energy?

Consider a system of two point charges in which positive test charge q’ moves in the field produced by stationary point charge q shown below in the figure.

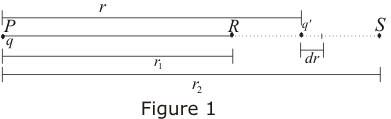
Charge q is fixed at point P and is displaced from point R to S along a radial line PRS shown in the figure. Let r₁ be the distance between points P and R and r₂ be the distance between P and S. The magnitude of the force on positive test charge as given by Coulomb’s law is:

If q’ moves towards S through a small displacement dr then work done by this force in making the small displacement dr. Therefore we have: dW=F·dr

Total work done by this force as test charge moves from point R to S i.e., from r₁ to r₂ is:

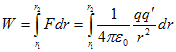
or

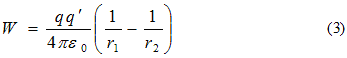
Thus, for this particular path work done on the test, charge q’ depends on the endpoints and not on the path is taken. Work done W in moving the test charge q’ from point R to S is equal to the change in potential energy in moving the test charge q’ from point R to S. Thus,

W=U(r₁)-U(r₂)                                          (4)

where

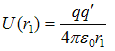
is the potential energy of test charge q’ when it is at point R and

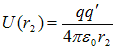
is the potential energy of test charge q’ when it is at point S.

You can download Electric Potential Energy and Electric Potential Cheat Sheet by clicking on the download button below

Electric Potential Energy of a System of Two Charges

Thus, the potential energy of test charge q’ at any distance r from charge q as follows

Equation 5 gives the electric potential energy of a pair of charges which depends on the separation between the charges, not on the location of charged particles. If we bring the test charge q’ from a very large distance such that r₂=∞ to some distance r₁=r then, we must do work against electric forces which is equal to increase in potential energy as given by equation 5.

Thus, the potential energy of a test charge at any point in the electric field is the work done against the electric forces to bring the charge from infinity to point under consideration.

Video on Electrostatics

The Electric Potential

Electric potential is the potential energy per unit charge. Thus, electrostatic potential at any point of an electric field is the potential energy per unit charge at that point. Electric potential is represented by letter V.
V=U/q’ or U=q’V                                             (6)

S.I. unit of electric potential is Volt which is equal to Joule per Coulomb. Thus, we have: 1 Volt = 1 JC^-1. In equation 4 if we divide both sides by q’ we have:

where V(r₁) is the potential energy per unit charge at point R and V<r₂₎ is potential energy per unit charge at point S and are known as a potential at points R and S respectively. Again consider figure 1. If point S in figure 1 would be at infinity then from equation 7

Since potential energy at infinity is zero, therefore, V(∞) = 0. Therefore, we have:

Hence electric potential at a point in an electric field is the ratio of the amount of work that we do in bringing test charge from infinity to that point to the magnitude of test charge. Dimensions of electric potential are [ML²T^-3A^-1].

Solved Example for You

Q: Four chargers q₁  =−0.02μC, q₂ = +0.04μC, q₃ =+0.02μC, and q₄ = − 0.04μC are at the four corners of a square of side 9cm. Then the potential at the centre of the square is:

1. 9 V
2. 3 V
3. 1.3 V
4. Zero

Solution: D) Since the potential is a scalar quantity, the net potential at any point is the sum of the individual potentials. Let r be the distance of each corner from the centre of the square. Thus we have the potential at the centre of the square = k/r [ (−0.02μC) + (0.04μC) + ( 0.02μC) + (−0.04μC ) ] = 0.