Geometric and Optical Isomerism

You have come across the concept of allotropes in Chemistry, haven’t you? Two elements with similar characteristics? In this chapter, we will cover a concept quite relatable to this. It is the concept of isomerism. We will also look at coordination number and its relation to isomerism. We will start with the basic concept of what isomerism is.

Suggested Videos

 

What is Isomerism?

Isomers are compounds having the same chemical formula but different structural arrangements. We find a number of isomers due to the variety of bond types and complicated formulae of many coordination compounds. In the below chapter, we will discuss the types of isomerism that these compounds exhibit.

1) Optical Isomerism

Optical isomers are those two compounds with the same chemical formula such that their mirror images are not superimposable on each other. Depending on the direction they rotate the plane of polarised light in a polarimeter, we have two forms of optical isomers. They are:

• Dextro Isomer: This rotates to right.
• Laevo Isomer: This rotates to left.

Let us now look at the concept of geometric isomerism.

2) Geometric Isomerism

In case of disubstituted complexes, the substituted groups could either be adjacent or opposite to each other. This leads to geometric isomerism. Thus, we can prepare square planar complexes such as [Pt(NH₃)₄Cl₂]  in two forms, cis and trans. When the chlorine atoms are adjacent to each other, we get the cis form. While when two chlorine atoms are opposite, we get the trans-form.

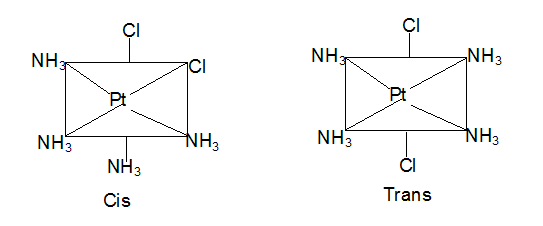
More about Geometric Isomerism and Coordination Number

• We find this type of isomerism in heteroleptic complexes. The main reason behind this would be the multiple geometric arrangements of ligands around the central metal atom.
• Coordination compounds with the coordination number of 4 and 6 mainly exhibit this type of isomerism.
• Square planar complexes are coordination compounds with coordination number 4 having [MX₂L₂] type formula, where X and L are unidentate ligands. The two ligands X could either be adjacent to each other in a cis isomer or opposite to each other to form a trans isomer.
  Square planar complexes with MABXL type formula show three isomers-two cis and one trans.
• Tetrahedral geometry does not display these isomers. However, octahedral complexes do show cis and trans isomerism. In complexes with formula [MX₂L₄] type, we can have the X ligands in the arrangement of cis or trans to each other.
• We also observe this type of isomerism when bidentate ligands L–L [e.g., NH₂ CH₂ CH₂ NH₂ (en)] are present in complexes with [MX₂(L–L)₂] type formula.
• There is another type of geometrical isomerism that we find in octahedral coordination entities with [Ma₃b₃] type formula. An example is [Co(NH₃)₃(NO₂)₃].

You can download Coordination Compounds Cheat Sheet by clicking on the download button below

Solved Example for You

Q: What are facial and meridional isomers?

Ans: Facial isomers are those where the three donor atoms of the same ligands occupy adjacent positions at the corners of an octahedral face. They have the ligands in the cis arrangement. We get the meridional isomers when the positions of the ligands are around the meridian of the octahedron. One pair is in trans arrangement here.