How does a cumulative frequency graph looks like?

The cumulative frequency is the running total of all the frequencies. At the graph, we can represent it with the help of a cumulative frequency polygon.

How can we calculate the cumulative frequency?

The cumulative frequency calculation can be done by adding each frequency from a frequency distribution table to the total sum of its predecessors.

What are the various types of the cumulative frequency?

There are 2 types of the cumulative frequency distributions, these are; Less than cumulative frequency distribution, this is achieved by adding successively all the frequencies of the total previous classes containing the class against which we have written it.

How can we plot the cumulative frequency?

A cumulative frequency diagram can be drawn by plotting the higher class boundary with the cumulative frequency.

Cumulative Frequency Curve : Concepts, Examples, Graphs

As we know, a picture speaks a thousand words. In the world of statics, graphs, in particular, are very important, as they help us make sense of the data and understand it better. So let us study the graphical representation of Cumulative Frequency Curve.

Videos

What is Cumulative Frequency?

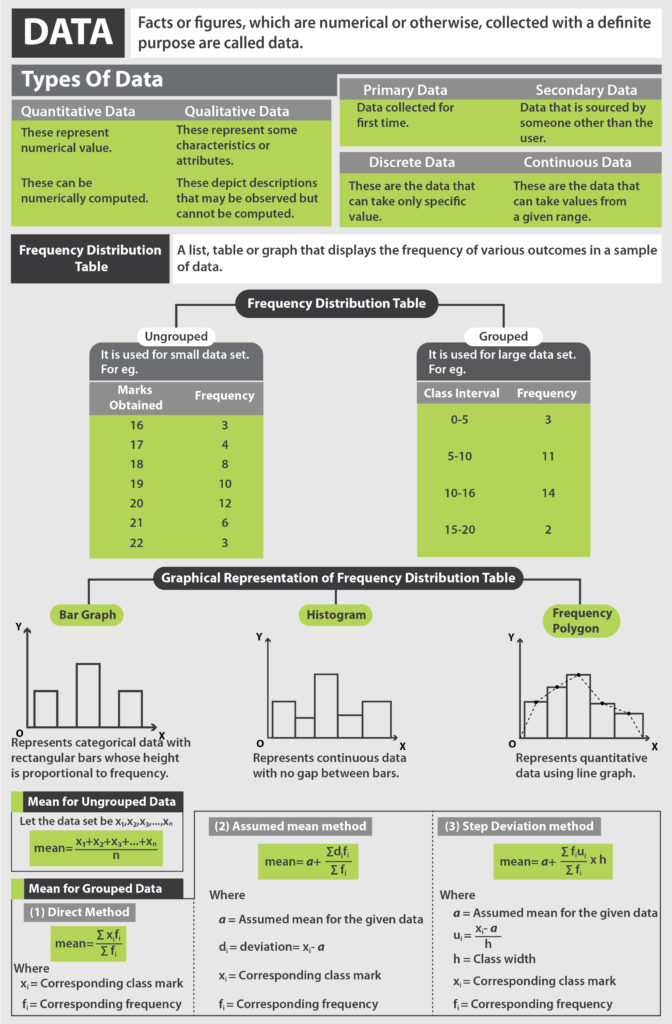
The frequency is the number of times an event occurs within a given scenario. Cumulative frequency is defined as the running total of frequencies. It is the sum of all the previous frequencies up to the current point. It is easily understandable through a Cumulative Frequency Table.

Marks	Frequency (No. of Students)	Cumulative Frequency
0 – 5	2	2
5 – 10	10	12
10 – 15	5	17
15 – 20	5	22

Cumulative Frequency is an important tool in Statistics to tabulate data in an organized manner. Whenever you wish to find out the popularity of a certain type of data, or the likelihood that a given event will fall within certain frequency distribution, a cumulative frequency table can be most useful. Say, for example, the Census department has collected data and wants to find out all residents in the city aged below 45. In this given case, a cumulative frequency table will be helpful.

Download the Cheat Sheet of Statistics by clicking on the button below

statistics cheat sheet

Browse more Topics under Statistics

Cumulative Frequency Curve

A curve that represents the cumulative frequency distribution of grouped data on a graph is called a Cumulative Frequency Curve or an Ogive. Representing cumulative frequency data on a graph is the most efficient way to understand the data and derive results.

Learn more about Frequency Polygon here.

There are two types of Cumulative Frequency Curves (or Ogives) :

More than type Cumulative Frequency Curve
Less than type Cumulative Frequency Curve

More Than Type Cumulative Frequency Curve

Here we use the lower limit of the classes to plot the curve.

How to plot a More than type Ogive:

In the graph, put the lower limit on the x-axis
Mark the cumulative frequency on the y-axis.
Plot the points (x,y) using lower limits (x) and their corresponding Cumulative frequency (y)
Join the points by a smooth freehand curve. It looks like an upside down S.

Learn more about Bar Graphs and Histogram here in detail.

Less Than Type Cumulative Frequency Curve

Here we use the upper limit of the classes to plot the curve.

How to plot a Less than type Ogive:

In the graph, put the upper limit on the x-axis
Mark the cumulative frequency on the y-axis.
Plot the points (x,y) using upper limits (x) and their corresponding Cumulative frequency (y)
Join the points by a smooth freehand curve. It looks like an elongated S.

Cumulative Graphs can also be used to calculate the Median of given data. If you draw both the curves on the same graph, the point at which they intersect, the corresponding value on the x-axis, represents the Median of the given data set.

Learn more about the Frequency Distribution here.