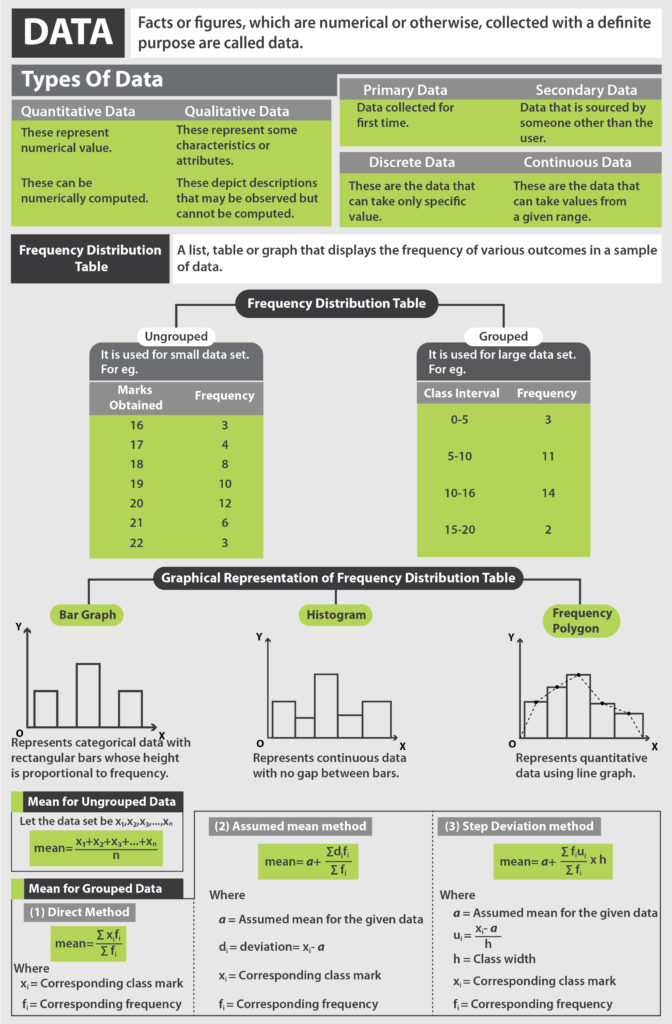
Did you know, the origin of the word “Mode” in fact comes from the French. It is derived from the French expression “a la mode”, meaning fashionable! Mode is nothing but the most popular number in any given population or data and an important measure of central tendency.
Videos
Mode
Mode is the value which occurs most frequently in a set of observations. Simply put, it is the number which is repeated most, i.e. the number with the highest frequency. In the field of statistics, it is an important tool to interpret data in a relevant manner. Now it is possible for the data set to be multimodal (have more than one mode) which means more than one observation has the same number of frequencies.
Example: Let us find the Mode of the following data
4, 89, 65, 11, 54, 11, 90, 56
Here in these varied observations the most occurring number is 11, hence the Mode = 11

Browse more Topics under Statistics
- Data
- Mean
- Median
- Bar Graphs and Histogram
- Cumulative Frequency Curve
- Frequency Distribution
- Frequency Polygon
- Range and Mean Deviation
- Range and Mean Deviation for Grouped Data
- Range and Mean Deviation for Ungrouped Data
- Variance and Standard Deviation
Download the Cheat Sheet of Statistics by clicking on the button below
Mode of Grouped Data
As we know that Mode is the most frequently occurring number of a data set. This is easily recognizable in an ungrouped dataset, but if the data set is presented in class intervals, this can get a bit tricky. So how can we calculate Mode of grouped data?
Steps to be followed to calculate the Mode are,
- Create a table with two columns
- In column 1 write your class intervals
- In column 2 write the corresponding frequencies
- Locate the maximum frequency denoted by fm
- Determine the class corresponding to fm , this will be your Modal class
- Calculate the Mode using given formula
Mode = L +\( \frac{f_m-f_1}{(2f_m-f_1-f_2)} \) × h
Where,
L = lower limit of Modal Class
fm = frequency of modal class
h = width of modal class
f1 = frequency of pre modal class
f2 = frequency of post modal class
Relation between Mean, Median, and Mode
There is an inter-relation between the measures of central tendency. Professor Karl Pearson has suggested an empirical relationship between Mean, Median, and Mode. Via this equation, if the values of two measures are known we can find the third measure. The equation is as follows
Mean – Mode = 3 [ Mean – Median ]

Solved Examples for You
Q: If the difference between the mode and median is 2, then find the difference between the median and mean.
Sol : We know, Mean – Mode = 3 [ Mean – Median ]
Mode = 3 x Median – 2 x Mean
Mode – Median = 2 x (Median – Mean)
2 =2 x (Median – Mean)
Median – Mean = 1
Q: The pre modal class and the post modal classrectangles have the same height. If the modal class is 40-60 , then what is the mode?
Sol : The modal class as given is 40-60
So, L = 40 and h = 20
Frequency of Modal Class = fm
Frequency of pre modal class = fm-1 = Frequency of post modal class
Mode = L +\( \frac{f_m-f_1}{(2f_m-f_1-f_2)} \) × h
= L +\( \frac{f_m-f_m-1}{(2f_m-f_m-1-f_m-1)} \) × h
= 40 + \( \frac{f_m-f_m-1}{(f_m-f_m-1)2} \)
= 40 + 10 = 50
Question- What is a mode in Math?
Answer- Mode is the value which takes place most commonly in a set of observations. In other words, it is the number which is repeated most, i.e. the number having the highest frequency. In the field of statistics, it is an essential tool to read data in an appropriate manner.
Question- What is the mode if there is no mode?
Answer- In that case, one has to add those two numbers together and then divide it by two to find the median. The mode of a data set is the number that occurs most frequently. If there is not a number that occurs more than any other, it means there is no mode for the data.
Question- What if you have two modes?
Answer- If a set has two modes then both of those numbers are said to be modes of the set. Thus, when this takes place, the set is referred to as bimodal.
Question- Is mode and modal the same?
Answer- We calculate the mode for individual numbers while the modal interval is calculated for ranges (intervals) of numbers.







Leave a Reply